Задача 1.
Дано пять разноцветных шаров, три из которых являются радиоактивными. Есть детектор, в который можно поместить два шара. При этом детектор активируется только если оба положенных в него шара радиоактивны. Как найти два радиоактивных шара, сделав не более трёх испытаний?
Задача 2.
Четверо рыцарей и лжецов — А, Б, В и Г — знают, что в их компании завелись шпионы — от 1 до 4. Между ними состоялся следующий разговор.
- А: «Я не шпион. Среди нас 2 лжеца».
- Б: «В точно шпион. Шпионов не больше 3».
- В: «А — шпион. Шпионов трое».
- Г: «Шпион только один. Все шпионы — лжецы».
Определите, кто из этих четверых шпионы.
Задача 3.
Разрежьте предложенную фигуру на три равные части по линиям сетки.
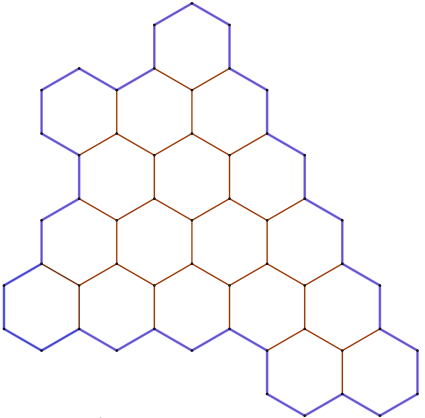
Задача 4.
У Сергея отпуск со 2 по 27 февраля. В первый день он пошёл гулять и прошёл 2 км. На следующий день он прошёл в 2 раза больше, чем в первый. В третий день прошёл в 2 раза больше, чем во второй. А вот в четвёртый день он целиком проспал. В следующие дни всё повторялось. Какое суммарное расстояние Серёжа прошёл за время своего отпуска?
Задача 5.
Можно ли так расставить числа от 1 до 8 в ряд, чтобы сумма любых трёх подряд идущих чисел была нечётной?
Задача 6.
Согласно Хроникам Кардура каждый орк, который сражался в битве при Норгасте, всегда говорит правду. Каждый орк, который дружит с эльфом, беден. Все орки, которые повстречали дракона и не имели при этом топора, были съедены. Каждый орк, у которого есть топор, богат. Однажды Шкрогг поведал своему другу Элеорину о том, как однажды встретился с драконом. Сражался ли Шкрогг в битве при Норгасте? (На всякий случай уточним, что Шкрогг — орк, а Элеорин — эльф.)
Задача 7.
Света составила пример на сложение: 2111 + 2021 = 4132. Попугай Рёмер изменил 3 цифры в слагаемых. Могла сумма новых чисел снова состоять из цифр 1, 2, 3 и 4?
Задача 8.
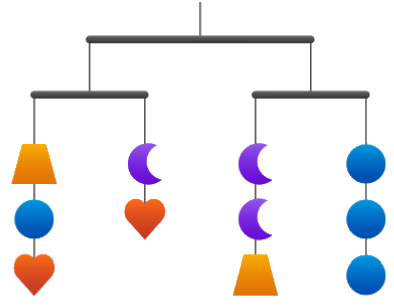
У Бори над кроваткой висит следующая игрушка, все планки которой находятся в равновесии. Во сколько раз круг тяжелее трапеции?