Задача 1.
По кругу стоят 16 натуральных чисел (не обязательно различных). Известно, что при любом разбиении их на 4 группы по 4 стоящих подряд числа сумма чисел во всех группах будет различной. Какая наименьшая сумма может быть у всех 16 чисел?
Задача 2.
Гретхен испекла прямоугольный торт, а затем разрезала его на попарно различные прямоугольные кусочки, сделав 2 вертикальных и 2 горизонтальных разреза. На одном из кусочков сидит пряничная лягушка. За один ход лягушка может перескочить на любой кусок торта, который находится в одной строке или в одном столбце с текущим, при условии что периметр нового куска больше. Какое наибольшее число прыжков лягушка может совершить?
Задача 3.
Два бегуна стартовали одновременно в разных концах трассы и побежали навстречу друг к другу с постоянными скоростями. Когда они встретились, у них взяли интервью.
- Первый сказал: «Я бежал со скоростью 3 м/c. Пробежал в 3 раза больше второго бегуна».
- Второй сказал: «Я бежал со скоростью 4 м/c. Длина трассы 4 км».
Известно, что один из бегунов постоянно путает две цифры (то есть вместо некоторой цифры 𝐴 всегда пишет некоторую другую цифру 𝐵? а вместо некоторой цифры 𝐵 всегда пишет некоторую другую цифру 𝐴). Найдите длину трассы.
Задача 4.
Можно ли разрезать квадрат 5 × 5 на пять пятиклеточных фигурок (пентамино) так, чтобы среди них не было прямоугольников 1 × 5, и при этом было четыре одинаковых фигуры?
Задача 5.
На рисунке ниже изображены три сообщающихся сосуда, в средний из которых налита вода.
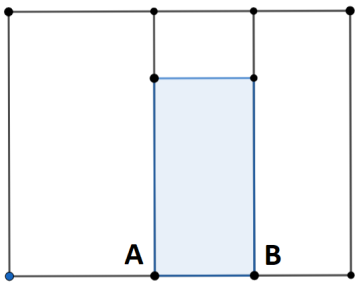
В точках 𝐴 и 𝐵 находятся маленькие отверстия, которые соединяют средний сосуд с боковыми и изначально закрыты. Витя открыл отверстие 𝐵, после чего уровень воды понизился в два раза. Затем он открыл отверстие 𝐴 и тогда уровень воды понизился ещё в два раза. Во сколько раз понизился бы уровень воды, если бы Витя изначально открыл только отверстие 𝐴?
Задача 6.
Робот стартовал в угловой клетке доски 6 × 6 и объехал её таким образом, что побывал в каждой клетке ровно один раз. Могло ли оказаться, что и среди его перемещений по вертикали было по одному перемещению на 5 клеток, 4 клетки, 3 клетки, 2 клетки и ровно 4 перемещения на одну клетку, а также среди его перемещений по горизонтали было по одному перемещению на 5 клеток, 4 клетки, 3 клетки, 2 клетки и ровно 3 перемещения на одну клетку?
Задача 7.
В чайхане собралось несколько купцов. Али богаче всех остальных, у него 7 верблюдов. Хасан беднее всех остальных, у него 4 верблюда. Сколько всего купцов собралось в чайхане, если в общей сложности у них 60 верблюдов?
Задача 8.
В классе учится 25 человек. У каждого из них есть 5 карточек, на каждой из которых написана одна из букв 𝑎, 𝑏 или 𝑐. Известно, что 13 детей могут составить слово 𝑎𝑎𝑎, но никто не может составить слово 𝑎𝑎𝑎𝑎. 12 детей могут составить слово 𝑏𝑏𝑏, но никто не может составить слово 𝑏𝑏𝑏𝑏. Также 8 детей могут составить слово 𝑎𝑏𝑐. Сколько детей могут составить слово 𝑎𝑏𝑎𝑏?

