Задача 1.
Из клетчатой доски вырезали 6 клеток, как показано на рисунке.
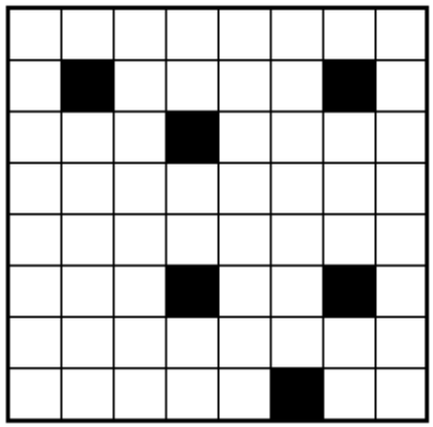
Имеется фишка, которая стоит в одной из уцелевших клеток доски. За ход фишку можно сдвинуть на одну клетку по горизонтали или вертикали, причём нельзя попадать в дырки. Можно ли по разу посетить все уцелевшие клетки и вернуться в исходную?
Задача 2.
В квадрате 5 × 5 разместили 81 доминошку. Каждая доминошка накрывает ровно две соседние клетки. Некоторые клетки накрыты сразу несколькими доминошками. Докажите, что найдутся три доминошки, накрывающие одни и те же две клетки.
Задача 3.
У Коли есть 2022 короткие нитки, на каждую из которых надето по пять бусин в следующем порядке: красная, синяя, красная, зелёная, красная. Коля связал из этих ниток одно большое ожерелье. Хулиган Вася может проделывать с ожерельем следующие три операции: вставить в любое место синюю бусину; вставить в любое место зелёную бусину; разрезать ожерелье в двух местах, а затем каждую из двух полученных ниток связать в отдельное новое ожерелье. Может ли Вася получить 54 ожерелья, которые все одинаковые?

