Задача 1.
У бабушки во дворе бегают куры, гуси и коровы. Если бабушка пустит во двор ещё 30 кур, то общее число птиц возрастёт в три раза. А если вместо этого бабушка выгонит со двора 10 гусей, то общее число животных уменьшится в два раза. Сколько коров бегает у бабушки во дворе?
Задача 2.
На дороге через равные промежутки расположены пункты 𝐴, 𝐵, 𝐶 и 𝐷. Почтальон Печкин хочет доставить посылку из пункта 𝐴 в пункт 𝐷 и вернуться обратно. Почтальон Свечкин хочет доставить посылку из пункта 𝐷 в пункт 𝐴 и вернуться обратно. Они стартовали одновременно и в первый раз встретились в пункте 𝐵. В каком месте произойдёт их вторая встреча?
Задача 3.
Можно ли в клетках таблицы 6 × 6 расставить крестики и нолики так, чтобы никакие три одинаковых знака не располагались подряд ни по горизонтали, ни по вертикали, ни по диагонали?
Задача 4.
Саша сложил 27 стандартных игральных кубиков в один куб 3 × 3 × 3. Он утверждает, что сумма очков на всех гранях его куба равна 290. Докажите, что Саша ошибся. (В стандартном игральном кубике грани расположены так, что сумма очков на каждой паре противоположных граней равна 7.)
Задача 5.
Есть три монеты весом 7 г и три монеты весом 8 г. Все монеты выглядят одинаково. Можно ли за два взвешивания на двухчашечных весах без гирь разделить монеты на три пары, каждая из которых весит 15 г?
Задача 6.
Миша и Маша катались на коньках. В понедельник Миша за 15 минут проехал на 840 метров больше, чем Маша проехала за 12 минут. Во вторник Маша проехала на 40 метров больше, чем Миша, но она каталась 8 минут, а Миша — 5 минут. Найдите скорости катания Миши и Маши. (Скорости во вторник остались прежними).
Задача 7.
Натуральное число называется порядочным, если в нём есть цифра, которая равна номеру своей позиции в этом числе. (Номера позиций считаются слева направо. Например, порядочным является число 5137, поскольку на третьем слева месте находится цифра 3.) Сколько существует порядочных трёхзначных чисел?
Задача 8.
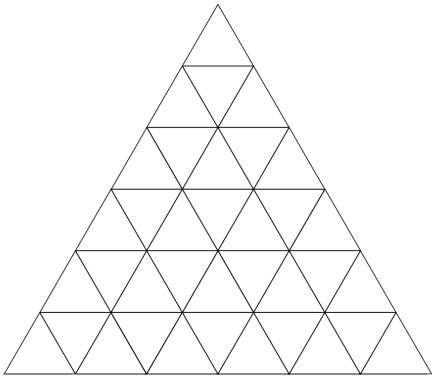
Муравейник имеет форму треугольника. В каждой ячейке живёт ровно один муравей, причём каждый из муравьёв либо всегда лжёт, либо всегда говорит правду. Однажды каждый из муравьёв заявил: «Среди моих соседей по стороне есть по меньшей мере один лжец». Какое наименьшее число муравьёв-лжецов может оказаться в муравейнике.