Задача 1.
Петя и Вася по очереди закрашивают клетки в прямоугольнике 3 × 6 (три строки и шесть столбцов). Петя начинает и каждым своим ходом закрашивает две соседние по вертикали клетки. Вася ходит вторым и каждым своим ходом закрашивает три соседние по горизонтали клетки. Повторно закрашивать клетку. Тот, кто не может сделать ход, проигрывает. Может ли кто-то из них гарантированно выиграть и если да, то кто и как?
Задача 2.
Сегодняшняя дата 22.02.2022 является палиндромом — восьмизначное число 22022022 читается одинаково слева направо и справа налево. А в каком году была последняя такая дата не в феврале, а в каком-то другом месяце?
Задача 3.
В марафоне участвовали 50 спортсменов, и все заняли разные места. На следующий день каждого из них спросили, какое место он занял, и каждый назвал одно из чисел от 1 до 50. Журналисты выяснили, что все названные числа отличались от реальных мест на 2. Докажите, что какие-то два числа никем названы не были.
Задача 4.
Некоторые из шести детей обменялись рукопожатиями, причём каждое рукопожатие было между мальчиком и девочкой. Четверо детей сделали по два рукопожатия, а остальные двое — по три. Должны ли эти двое были пожать руку друг другу?
Задача 5.
Четверо рыцарей и лжецов — А, Б, В и Г — знают, что в их компании завелись шпионы — от 1 до 4. Между ними состоялся следующий разговор.
- А: «Я не шпион. Среди нас 2 лжеца».
- Б: «В точно шпион. Шпионов не больше 3».
- В: «А — шпион. Шпионов трое».
- Г: «Шпион только один. Все шпионы — лжецы».
Определите, кто из этих четверых шпионы.
Задача 6.
Разрежьте предложенную фигуру на три равные части по линиям сетки.
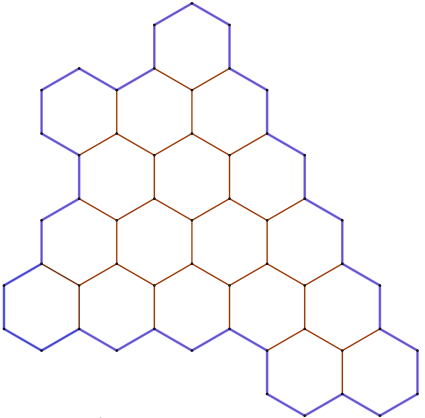
Задача 7.
В санаторий приехали несколько архитекторов, бухгалтеров и врачей, некоторые из которых дружат между собой. Известно, что у каждого архитектора среди друзей врачей в три раза больше, чем бухгалтеров. А у каждого бухгалтера среди друзей врачей в шесть раз больше, чем архитекторов. Оказалось, что у каждого врача среди друзей бухгалтеров в 𝑛 раз больше, чем архитекторов. Определите, чему равно 𝑛.
Задача 8.
Света составила пример на сложение: 2111 + 2021 = 4132. Попугай Рёмер изменил 3 цифры в слагаемых. Могла сумма новых чисел снова состоять из цифр 1, 2, 3 и 4?

