Задача 1.
Незнайка записал несколько последовательных натуральных чисел. Знайка посчитал, что при этом было использовано 6 нулей, 6 единиц, 16 двоек, одна тройка и одна четвёрка. Сколько чисел мог написать Незнайка?
Задача 2.
Незнайка составил ребус: КЛЮКВА + ВОДА = КОМПОТ, и утверждает, что сумма всех цифр в примере равна 54. Может ли Незнайка оказаться прав?
Задача 3.
Гретхен испекла прямоугольный торт, а затем разрезала его на попарно различные прямоугольные кусочки, сделав 8 вертикальных и 8 горизонтальных разрезов. На одном из кусочков сидит пряничная лягушка. За один ход лягушка может перескочить на любой кусок торта, который находится в одной строке или в одном столбце с текущим, при условии что периметр нового куска больше. Какое наибольшее число прыжков лягушка может совершить?
Задача 4.
Два бегуна стартовали одновременно в разных концах трассы и побежали навстречу друг к другу с постоянными скоростями. Когда они встретились, у них взяли интервью.
- Первый сказал: «Я бежал со скоростью 3 м/c. Пробежал в 3 раза больше второго бегуна».
- Второй сказал: «Я бежал со скоростью 4 м/c. Длина трассы 4 км».
Известно, что один из бегунов постоянно путает две цифры (то есть вместо некоторой цифры 𝐴 всегда пишет некоторую другую цифру 𝐵? а вместо некоторой цифры 𝐵 всегда пишет некоторую другую цифру 𝐴). Найдите длину трассы.
Задача 5.
Утром в пруду плавало 150 амёб: 50 синих, 50 красных и 50 зелёных. Время от времени амёбы встречаются. Если встречаются синяя и красная амёба, то взамен их появляются красная и зелёная амёбы. Если встречаются 3 красные и зелёная амёба, то они превращаются в красную и синюю амёбу. Если встречаются две зелёные амёбы, то взамен их появляются две синие амёбы, а если вместе встречаются вместе три попарно разноцветные амёбы, то они превращаются в две зелёные амёбы. К концу дня в пруду плавало 100 амёб. Сколько среди них могло быть красных?
Задача 6.
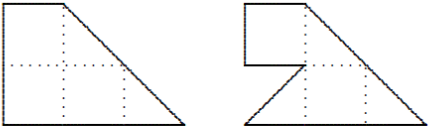
Отрежьте от левой фигурки часть и добавьте её к правой фигурке так, чтобы обе новых фигурки имели ось симметрии. Добавляемую часть можно поворачивать и переворачивать.
Задача 7.
По кругу отмечены 2022 точки. Двое по очереди делают ходы. За ход можно соединить две отмеченные точки красным отрезком. Выигрывает тот игрок, после хода которого впервые появится треугольник с красными сторонами и вершинами в изначально отмеченных точках. Кто из игроков, первый или второй, может выиграть вне зависимости от ходов соперника?
Задача 8.
Антонио написал на доске четырёхзначное число. Борисио посчитал все суммы соседних цифр в этом числе, они оказались попарно различными двузначными числами. Какое наименьшее число мог записать Антонио на доске?

