Задача 1.
Костя придумал число, произведение цифр которого равно 72, а сумма цифр — 18. Может ли оно быть пятизначным?
Задача 2.
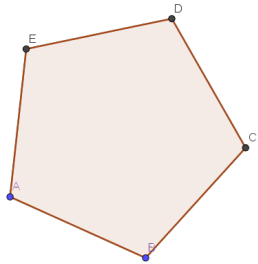
Правильным называется такой многоугольник, у которого все стороны одинаковы и все углы равны. Можно ли нарисовать 4 правильных пятиугольника так, чтобы любые два из них имели ровно две общих вершины?
Задача 3.
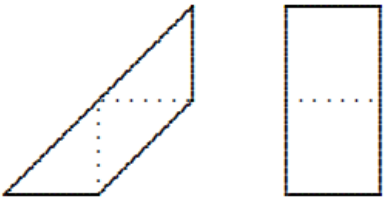
Незнайка вырезал из клетчатой бумаги два четырёхугольника, изображённых на рисунке ниже. Теперь он хочет вырезать ещё одну фигурку, которую можно будет добавить к каждой из первых двух таким образом, чтобы получившаяся фигура имела ось симметрии. Обязательно ли третья фигурка Незнайки будет иметь ось симметрии?
Задача 4.
Можно ли числа от 18 до 31 расставить по кругу так, чтобы произведение любых двух соседних чисел было меньше 600?
Задача 5.
Сегодняшняя дата 22.02.2022 является палиндромом — восьмизначное число 22022022 читается одинаково слева направо и справа налево. Через сколько лет впервые наступит (и вообще наступит ли) дата, которая является одновременно и восьмизначным палиндромом, и простым числом?
Задача 6.
На фазенде дона Никиты, которая по-прежнему представляет собой прямоугольник 3 × 5, вновь завёлся крот (изначально он сидит в одной из клеток). У дона Никиты отобрали его оружие из прошлой задачи, поэтому дон Никита купил двухстволку, из которой можно выстрелить снотворным в две соседние клетки фазенды. Дон хочет поймать крота, поэтому стреляет по огороду из двухстволки. Если после выстрела дон не попал в крота, то крот, услышав выстрел, пугается и переползает в соседнюю по стороне клетку. Также известно, что если после прошлого выстрела крот переползал по вертикали, то в этот раз он будет уползать по горизонтали. И наоборот, если до этого он переползал по горизонтали, то в следующий раз он будет уползать по вертикали. Может ли дон Никита гарантировано попасть в крота, сделав какое-то фиксированное количество выстрелов?

