Задача 1.
Карлсон пришёл в магазин закупиться вареньем. Банка малинового варенья стоила 115 рублей, банка вишнёвого — 175 рублей, а банка клюквенного — 195 рублей. Известно, что Карлсон купил 100 банок варенья, при этом малинового и вишнёвого варенья было куплено поровну, а всего Карлсон заплатил за покупку 16 тысяч рублей. Сколько варенья каждого вида купил Карлсон?
Задача 2.
Женя записал в каждой клетке таблицы 3 × 3 по одному числу, как на рисунке. Можно ли переставить числа, чтобы в каждом квадратике 2 × 2 суммы чисел были различными?
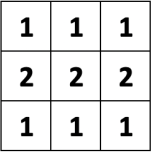
Задача 3.
К следователю привели троих обвиняемых, из которых ровно один — преступник, и троих свидетелей, из которых ровно один — лжесвидетель. Лжесвидетель всегда говорит неправду, а остальные говорят правду. Знающий всё вышеописанное следователь может спросить у любого свидетеля про любого обвиняемого: «Это преступник?» Как следователю с помощью 3 вопросов найти преступника?
Задача 4.
Варя нарисовала на треугольной сетке ромб площадью 32 маленьких треугольника (см. рисунок). Гоша утверждает, что этот ромб возможно разрезать по линиям сетки на две фигуры так, чтобы периметры у фигур были равными, а площади полученных фигур отличались более чем на 9 маленьких треугольников. Прав ли Гоша?
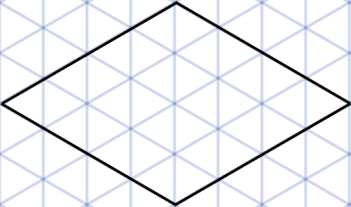
Задача 5.
Пётр Тормоз вышел на прогулку из пункта 𝐴 в пункт 𝐵 со скоростью 2 км/ч. Через 5 минут после этого вслед за ним из пункта 𝐴 вышел Иван Скороход со скоростью 8 км/ч, а из пункта 𝐵 навстречу ему – его брат Фёдор Скороход с такой же скоростью. Каждый раз, доходя до пунктов 𝐴 и 𝐵, братья сразу поворачивали и шли назад. Это продолжалось до тех пор, пока Пётр не пришёл в пункт 𝐵. Кто из братьев чаще оказывался с Петром в одной точке, если расстояние между 𝐴 и 𝐵 не меньше 10 км?
Задача 6.
Три мальчика разговаривают после урока:
- Антон: Я получил за контрольную 5!
- Борис: Я написал работу не хуже, чем Вадим.
- Вадим: Антон написал контрольную на 4.
- Антон: Кстати, Борис написал её на 4.
- Борис: Вадим получил 4.
- Вадим: Я получил 5.
Известно, что один мальчик оба раза солгал, а остальные сказали правду. Определите, кто из них написал контрольную работу на 4.
Задача 7.
В какое наибольшее количество цветов можно раскрасить клетки прямоугольника 2 × 4 так, чтобы соседние по стороне клетки были раскрашены в разные цвета и каждая клетка имела соседей ровно двух цветов?
Задача 8.
Имеет ли данный ребус хотя бы одно решение: СИЛА + МУЛ = МУЛАТ? Разные буквы обозначают разные цифры, а одинаковые буквы – одинаковые цифры.

