Задача 1.
У Гоши было 1000 деревянных дощечек размером 2 × 2. Гоша вырезал лазером из некоторых дощечек по линиям сетки 500 маленьких квадратов 1 × 1. При этом из одной дощечки он, конечно, мог вырезать от 1 до 4 квадратов 1 × 1. Докажите, что после вырезания из всех оставшихся частей дощечек можно собрать какой-нибудь прямоугольник без дырок.
Задача 2.
Незнайка взял стопку бумаги и сложил её пополам, получив тем самым стопку из нескольких вложенных друг в друга двойных листов. После этого он разрезал полученную стопку двумя прямыми разрезами, параллельными краям листов. Когда Незнайка развернул все сложенные части, у него получилось 60 прямоугольных кусочков. Сколько листов могло быть первоначально в стопке?
Задача 3.
Ананас дороже манго на 2163 рубля, но для них продавец использовал один и тот же ценник с четырёхзначным числом. Сколько мог стоить ананас? (На картинке приведены примеры написания всех цифр продавцом.)
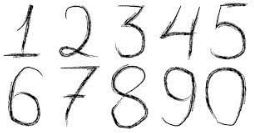
Задача 4.
Арина продавала на блошином рынке алмазики, несколько штучек. Торговля не шла, и она снизила цену алмазика на 20 рублей. Продав по этой цене четыре штучки, она снизила цену ещё на 20 рублей. По новой цене она продала ещё десять штук, после чего снизила цену ещё на 20 рублей и продала оставшиеся алмазики. В результате она заработала столько же денег, сколько заработала бы, продав изначально все алмазики на 40 рублей дешевле первоначальной цены. Сколько было алмазиков у Арины?
Задача 5.
Разрежьте прямоугольник 3 × 8 на 3 попарно различные 8-клеточные фигуры полимино, из которых можно сложить прямоугольник 4 × 6.
Задача 6.
Бёлка разложила 100 орехов по трём дуплам: № 1, № 2 и № 3. Известно, что в дупле № 1 изначально было меньше орехов, чем в дупле № 2, а в дупле № 2 было меньше орехов, чем в дупле № 3. Дятел может переложить из дупла с большим номером в дупло с меньшим номером 2 или 3 ореха. Верно ли, что Дятел своими действиями может добиться того, чтобы разница между количествами орехов в любых двух дуплах отличалась не более, чем на 1?
Задача 7.
Олег расставил в клетках таблицы 2 × 7 натуральные числа. Катя подсчитала суммы чисел во всех строчках и всех столбцах. Катя утверждает, что эти суммы равны числам от 10 до 18 (каждое число является какой-то суммой). Докажите, что Катя ошиблась.
Задача 8.
Четверо детей разного роста обсуждали, кто кого выше.
- Антон: «Я выше ровно двоих из вас!»
- Борис: «Я не самый низкий».
- Вова: «Я выше Антона. Гоша выше меня».
- Гоша: «Есть ровно двое людей, которые выше Бори!»
Каждый мальчик был либо рыцарем, который говорит только правду, либо лжецом, который врёт во всех утверждениях. Выстройте детей по росту, если среди них было хотя бы 3 рыцаря.

