Задача 1.
В строчку выписали без пробелов натуральные числа, начиная с 2024: 202420252026 . . . В какой-то момент в этой строке впервые встретился кусок «2023». Какие три цифры идут после него?
Задача 2.
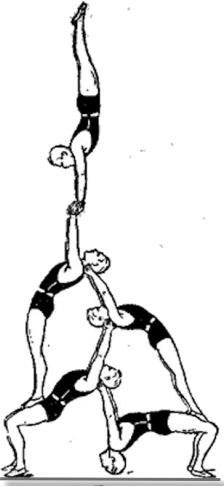
В гимнастической фигуре участвует 5 мальчиков (см. рисунок). Известно, что голова Ивана выше головы Вовы. При этом Вова не касается ни пола, ни Миши, а вот Миша пола касается. Оставшихся двух ребят зовут Роберт и Илья, причём Илья смотрит прямо в спину Роберту. Найдите имена всех детей на картинке.
Задача 3.
Коля задумал нечётное натуральное число, а затем прибавил к нему следующие после него 5 чётных чисел в натуральном ряду. Известно, что полученная сумма оказалась больше 2023, но меньше 2043. Какое число мог задумать Коля? (Пояснение: если он задумал 5, то прибавить нужно 6, 8, 10, 12 и 14.)
Задача 4.
Можно ли представить число 2023 в виде суммы нескольких трёхзначных чисел-палиндромов? Среди чисел-палиндромов в сумме могут быть равные.
Пояснение: Число называется палиндромом, если от перестановки цифр в обратном порядке оно не меняется. Например, числа 1331 и 606 — палиндромы, а 1011 и 660 — не палиндромы.
Задача 5.
По кругу лежит 6 монет, среди которых 3 настоящие и 3 фальшивые. Настоящие монеты весят одинаково и фальшивые весят одинаково, при этом фальшивые и настоящие монеты отличаются по весу. Варя утверждает, что фальшивые и настоящие монеты в кругу чередуются. Как Гоше за 2 взвешивания на чашечных весах проверить, верны ли слова Вари?
Задача 6.
Мама дала трём своим сыновьям, Антону, Боре и Пете, 11 конфет. Мальчики узнали свои количества конфет и выяснили следующее. Если Антон отдаст хотя бы 2 своих конфеты Пете, то у Пети точно будет больше половины всех конфет. Если же изначально Петя отдаст хотя бы 1 свою конфету Боре, то у Бори будет больше половины всех конфет. Сколько конфет может быть у каждого мальчика?
Задача 7.
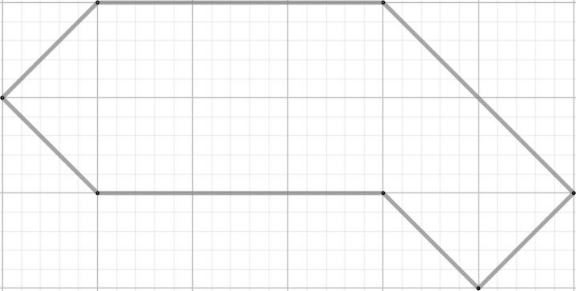
Разрежьте фигуру на рисунке на 4 равных кусочка. Резать можно не только по линиям сетки!
Задача 8.
Художник Мазимир Калевич закрасил в прямоугольнике 2 × 4 в чёрный цвет 4 клеточки, а остальные 4 остались незакрашенными белыми. Верно ли, что при любой раскраске в квадрате найдётся трёхклеточный уголок, в котором ровно 2 закрашенные клетки?

