Задача 1.
Числа 1, 2, . . . , 64 расставлены в каком-то порядке на доске 8 × 8. Докажите, что можно указать хотя бы два квадрата 2 × 2, сумма чисел в каждом из которых больше 100.
Задача 2.
Саша написала на 4 карточках из плотной непрозрачной бумаги числа от 1 до 4 (каждое по разу на одной из карточек). Затем она выложила карточки по кругу на столе в каком-то порядке числами вниз (то есть все карточки сверху неотличимы). После этого к столу подошёл Никита; ему разрешается за 1 операцию указать на любые 2 карточки, чтобы Саша честно ответила, на какой карточке число больше, и на сколько. Покажите, как за 3 операции Никите определить числа на всех карточках.
Задача 3.
Четыре прямых проведены так, что никакие две не параллельны и никакие три не пересекаются в одной точке. Они разделили плоскость на 11 частей (см. рисунок). Расставьте в эти части числа от 1 до 11 так, чтобы для каждой прямой суммы чисел по разные стороны от неё были равными. Каждое число, конечно, используется 1 раз.
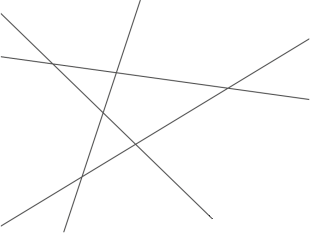
Задача 4.
По кругу сидело пять человек, каждый из которых был рыцарем или лжецом. Известно также, что было хотя бы по одному человеку обоих типов. Каждому из сидящих за столом задали вопрос: «Сколько среди двух твоих соседей рыцарей?» На этот вопрос не были даны никакие ответы, кроме, возможно, «Два» и «Ноль». Сколько рыцарей могло сидеть в круге?
Задача 5.
Из 10 различных цифр составлены 4 числа. Самое большое из них составлено из самых маленьких цифр, а самое маленькое число делится на 17. Найдите сумму двух средних чисел.
Задача 6.
Клетки доски 7 × 7 окрашены в шахматном порядке так, что углы окрашены в чёрный цвет. Разрешается перекрашивать в противоположный цвет любой уголок из трёх клеток. Можно ли с помощью таких операций перекрасить всю доску в белый цвет?
Задача 7.
Никита приехал в отпуск на остров (время прибытия и отъезда произошло в неизвестное время суток). Каждый раз, встречая закат или восход на острове, Никита плакал. Зато в каждый полдень на острове Никита смеялся. Известно, что всего за время отпуска Никита плакал 114 раз. Сколько раз он мог смеяться во время отпуска?
Пояснение: Восход на острове происходит задолго до полудня, а заход через некоторое продолжительное время после полудня.
Задача 8.
Каждый день, когда Миша приходит в школу, он получает 1 двойку, 2 тройки, 5 четвёрок и 6 пятёрок. Каждый день, когда Маша приходит в школу, она получает 5 двоек, 2 тройки, 5 четвёрок и 9 пятёрок. Известно, что Миша и Маша несколько раз сходили в школу и получили 3000 пятёрок. Сколько всего двоек, троек и четвёрок получили дети? (Миша и Маша могут прогуливать школу в разные дни.)

