Задача 1.
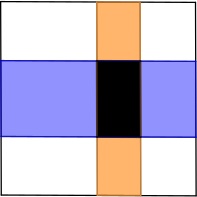
Два прямоугольника одинаковой площади, синий и оранжевый, расположены в большом прямоугольнике, как показано на рисунке. В пересечении синего и оранжевого прямоугольников получился прямоугольник, площадь которого в 100 раз меньше площади большого. А во сколько раз его периметр меньше периметра большого?
Задача 2.
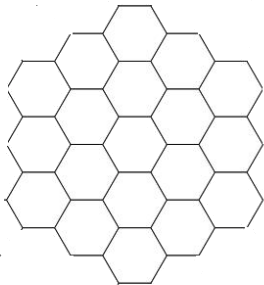
У Кости есть фигура, составленная из шестиугольников со стороной 1 (см. рисунок). Он хочет закрасить некоторые стороны шестиугольников красным цветом так, чтобы красные отрезки образовали замкнутую несамопересекающуюся ломаную. Какая наибольшая длина может быть у такой ломаной?
Задача 3.
На доске было написано натуральное число. Пришла Машенька, умножила его на 16 и записала вместо него. Прибежал Вовочка и стёр последнюю цифру. Пришла Настенька и умножила число на доске на 6. Вовочка снова стёр последнюю цифру. Могло ли после этого на доске оказаться первоначальное число?
Задача 4.
Арина продавала на блошином рынке алмазики, несколько штучек. Торговля не шла, и она снизила цену алмазика на 20 рублей. Продав по этой цене четыре штучки, она снизила цену ещё на 20 рублей. В результате она продала все алмазики и заработала столько же денег, сколько заработала бы, продав все алмазики на 32 рубля дешевле, чем планировала. Сколько алмазиков было у Арины?

