Задача 1.
В коробке лежат 15 красных шариков, 20 синих, 30 зелёных и 40 белых. Серёжа вытаскивает шарики, пока у него не окажется разное количество шариков каждого из четырёх цветов (изначально считается, что у него одинаковое количество шариков каждого цвета: их нет). Какое наибольшее количество шариков может вытащить Серёжа?
Задача 2.
На бесконечном клетчатом поле в клетке с координатами (0; 0) сидит лягушка, которая умеет прыгать на соседнюю клетку (в том числе по диагонали). Сколькими способами она может добраться за шесть прыжков до клетки с координатами (6; 3)?
Задача 3.
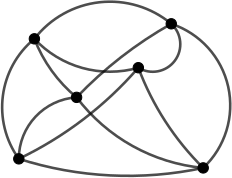
Кощей Бессмертный борется с волшебным шиповником. Шиповник состоит из цветов и соединяющих их стеблей (см картинку). За один удар мечом Кощей может обрубить все стебли, ведущие в один цветок, но сразу же после этого вырастают стебли во все цветы, которые до удара не были с ним соединены. Шиповник погибнет, если у него останется меньше четырёх стеблей. Сможет ли Кощей победить?
Задача 4.
Таблица из 11 строк и 100 столбцов заполнена числами — по одному числу в клетке. Известно, что в каждой строке, кроме последней, есть хотя бы 91 число, которое больше, чем число под ним (в том же столбце следующей строки). Может ли в последней строке найтись 91 число, которое больше, чем число в том же столбце в первой строке?
Задача 5.
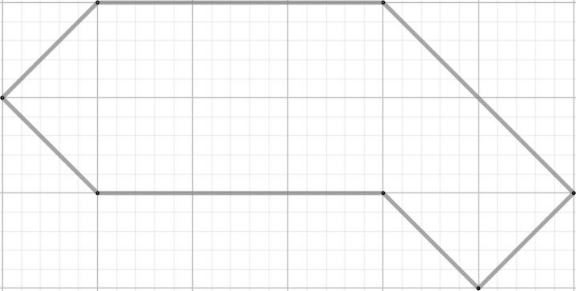
Докажите, что фигуру на рисунке можно разрезать на любое чётное количество равных кусочков.
Задача 6.
В начале урока учитель спросил детей «В смысле?» и получил ответы: «В прямом», «В переносном», «В коромысле». В конце урока он задал тот же вопрос и получил тот же набор ответов. Оказалось, что тех, кто хотя бы раз ответил «В коромысле», и тех, кто так не отвечал, поровну. Ответивших хотя бы раз «В прямом» оказалось вдвое больше тех, кто ни разу так не отвечал. И, наконец, тех, кто ответил «В переносном», было в три раза больше, чем тех, кто так не отвечал. Во сколько раз меньше ответивших одинаково по сравнению с теми, кто поменял свой ответ?

