Цветик-семидесятицветик имеет 30 красных и 40 зелёных лепестков. Лепестки можно срывать только парами. Если сорвать два красных лепестка, то вырастут красный и зелёный. Если сорвать два зелёных, то вырастет красный. А если сорвать красный и зелёный, то вырастут два зелёных. Девочка Женя 60 раз срывала по два лепестка, и красных лепестков совсем не осталось. А сколько осталось зелёных лепестков?

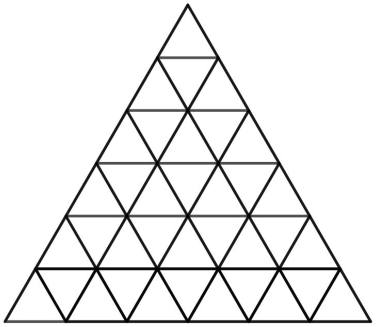
Двое играют в игру на треугольной доске, разделённой на 36 треугольничков (см. рисунок). Своим первым ходом первый игрок может поставить игральную фишку на любую маленькую треугольную клетку кроме тех, что находятся в углах большого треугольника. После этого игроки начинают по очереди делать ходы этой фишкой, при этом каждый раз нужно перемещать фишку в соседнюю по стороне треугольную клетку. Кроме того, запрещено посещать более 1 раза одну и ту же треугольную клетку (в том числе первоначальную). Тот, кто не может сделать ход, проигрывает. Кто из игроков может одержать победу вне зависимости от действий другого игрока?

На большом сборном концерте каждый из трёх звёзд-исполнителей должен исполнить три песни. При этом звезды потребовали от организаторов следующее: Гриша: Я хочу открывать концерт, а также петь сразу вслед за Вовой чаще, чем он будет петь сразу вслед за мной. Вова: Я хочу выступать сразу после Фили чаще, чем он будет петь после меня. А ещё я не хочу петь в самом конце. Филя: Зато в конце хочу петь я. Но с одним условием: я должен петь после Вовы только если он поёт не после Гриши. Сумеют ли организаторы удовлетворить все эти капризы?

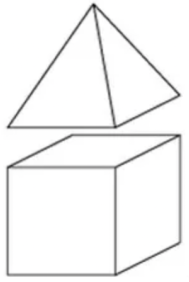
Матвей строит бассейн: по периметру прямоугольником он ставит на землю бетонные кубы вплотную друг к другу, а на некоторые из них сверху ещё ставит пирамидку (см. рисунок). Когда он с гордостью оглядел своё творение, он заметил, что у его бассейна 48 видимых граней (те грани, которые примыкают к земле или касаются друг друга, конечно, не видны). Чему могло быть равно общее количество использованных блоков (суммарное число кубов и пирамидок)?

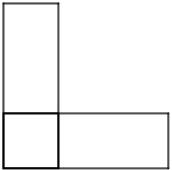
Уголком называется фигура, состоящая из двух одинаковых прямоугольников, примыкающих к соседним сторонам квадрата. Докажите, что два разных уголка не могут иметь одинаковую площадь и одинаковый периметр.

Из различных цифр от 1 до 9 составили три трёхзначных числа. Могут ли они все делиться на 36?

По кругу стояли 10 человек, каждый из них был рыцарем или лжецом. Каждому в круге задали вопрос: «Сколько рыцарей среди твоих двух соседей?» Было получено 10 различных ответов. Сколько рыцарей могло быть в круге?

Назовём пару ладей, стоящих на клетчатой доске, «хорошей», если на этой доске есть пустая клетка, которую обе эти ладьи бьют. На доску 9 × 9 поставили 14 ладей. Докажите, что на доске найдётся пара ладей, которая не является «хорошей». (Ладья бьёт пустую клетку, если они находятся в одной строке или столбце, а между ними нет других фигур.)