Задача 1.
У Гоши было 1000 деревянных дощечек размером 2 × 2. Гоша вырезал лазером из некоторых дощечек по линиям сетки 500 маленьких квадратов 1 × 1. При этом из одной дощечки он, конечно, мог вырезать от 1 до 4 квадратов 1 × 1. Докажите, что после вырезания из всех оставшихся частей дощечек можно собрать какой-нибудь прямоугольник без дырок.
Задача 2.
Петя и Вася задумали сыграть в игру. Сначала Петя пишет на доске 9-значное число, в котором нет одинаковых цифр. Вася может один раз изменить любую цифру в этом числе, но не более, чем на 2 (при этом цифры зациклены, то есть цифру 9 можно менять на 7, 8, 0 и 1). Если после хода Васи на доске окажется простое число, то он выиграет, иначе выигрывает Петя. Кто из игроков может обеспечить себе победу вне зависимости от действий другого игрока?
Задача 3.
Незнайка взял стопку бумаги и сложил её пополам, получив тем самым стопку из нескольких вложенных друг в друга двойных листов. После этого он разрезал полученную стопку двумя прямыми разрезами, параллельными краям листов. Когда Незнайка развернул все сложенные части, у него получилось 60 прямоугольных кусочков. Сколько листов могло быть первоначально в стопке?
Задача 4.
Ананас дороже манго на 2163 рубля, но для них продавец использовал один и тот же ценник с четырёхзначным числом. Сколько мог стоить ананас? (На картинке приведены примеры написания всех цифр продавцом.)
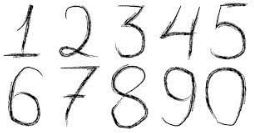
Задача 5.
Взвод получил для солдат 10 одинаковых шинелей размера 6. Поскольку солдаты не все одинаковы, шинели необходимо исправить на размерный ряд от 1 до 10 по одной каждого размера. Разрешается взять две любые шинели и из них получить две другие, уменьшив размер одной на 2 пункта и увеличив размер другой на 1 пункт. Можно ли добиться желаемого?
Задача 6.
Разрежьте прямоугольник 3 × 8 на 3 попарно различные 8-клеточные фигуры полимино, из которых можно сложить прямоугольник 4 × 6.
Задача 7.
Бёлка разложила 100 орехов по трём дуплам: № 1, № 2 и № 3. Известно, что в дупле № 1 изначально было меньше орехов, чем в дупле № 2, а в дупле № 2 было меньше орехов, чем в дупле № 3. Дятел может переложить из дупла с большим номером в дупло с меньшим номером 2 или 3 ореха. Верно ли, что Дятел своими действиями может добиться того, чтобы разница между количествами орехов в любых двух дуплах отличалась не более, чем на 1?
Задача 8.
Незнайка устроился работать почтальоном. Перед первым рабочим днём ему сообщили протяженности маршрутов 𝐴𝐵𝐸𝐷, 𝐴𝐹 и 𝐶𝐵𝐸𝐹 𝐴 в каком-то порядке: 24 км, 36 км и 12 км. Также известно, что 𝐴𝐶𝐷𝐹 — квадрат, а 𝐵𝐶𝐷𝐸 — прямоугольник. Какой длины маршрут 𝐴𝐵𝐸𝐹 , если известно что длина маршрута 𝐶𝐵𝐸𝐷 равна 16 км?


