Задача 1.
Используя цифры от 0 до 9 по одному разу, составили несколько простых чисел. Может ли их сумма быть равна 900?
Задача 2.
В коробке лежат 10 красных шариков, 20 синих и 30 зелёных. Серёжа вытаскивает шарики, пока у него не окажется разное количество шариков каждого из трёх цветов (изначально считается, что у него одинаковое количество шариков каждого цвета: их нет). Какое наибольшее количество шариков может вытащить Серёжа?
Задача 3.
На бесконечном клетчатом поле в клетке с координатами (0; 0) сидит лягушка, которая умеет прыгать на соседнюю клетку (в том числе по диагонали). Сколькими способами она может добраться за шесть прыжков до клетки с координатами (6; 4)?
Задача 4.
КЕРНИТ + АЛМАЗ + НАЛИМ + КАРНИЗ = 15991. Чему может быть равно число МАЛИНА? (Одинаковыми буквами заменены одинаковые цифры, разными — разные. Некоторые буквы могут заменять цифры 1, 5 или 9.)
Задача 5.
В строчку выписали без пробелов натуральные числа, начиная с 2024: 202420252026 . . . В какой-то момент в этой строке впервые встретился кусок «2023». Какие три цифры идут после него?
Задача 6.
В любой группе из трёх приехавших в лагерь школьников либо все трое попарно знакомы (то есть все знают всех), либо знакома только одна пара людей (а третий человек людей из пары не знает). По приезде в лагерь у Андрея оказалось 50 друзей, а у Бориса – 40. Сколько школьников приехало в лагерь?
Задача 7.
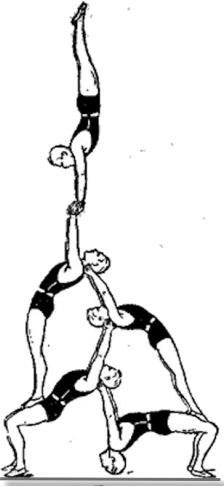
В гимнастической фигуре участвует 5 мальчиков (см. рисунок). Известно, что голова Ивана выше головы Вовы. При этом Вова не касается ни пола, ни Миши, а вот Миша пола касается. Оставшихся двух ребят зовут Роберт и Илья, причём Илья смотрит прямо в спину Роберту. Найдите имена всех детей на картинке.
Задача 8.
Можно ли представить число 2023 в виде суммы нескольких трёхзначных чисел-палиндромов? Среди чисел-палиндромов в сумме могут быть равные.
Пояснение: Число называется палиндромом, если от перестановки цифр в обратном порядке оно не меняется. Например, числа 1331 и 606 — палиндромы, а 1011 и 660 — не палиндромы.

