Задача 1.
Числа 1, 2, . . . , 64 расставлены в каком-то порядке на доске 8 × 8. Докажите, что можно указать хотя бы два квадрата 2 × 2, сумма чисел в каждом из которых больше 100.
Задача 2.
Король назначил своим троим мудрецам номера от 1 до 3, но не сказал никому его номер, а предложил определить его в испытании. Король посадил мудрецов в круг и выдал каждому две карточки, на которых написаны номера их соседей по кругу. Каждый мудрец, не глядя в карточки, приклеил одну из них на лоб своему левому соседу, а вторую — правому. Все мудрецы видят карточки на всех лбах, кроме своего. Сколько из них гарантированно смогут определить свой номер?
Задача 3.
С натуральным числом проделывают следующую операцию: его делят на самый маленький из его простых делителей и одновременно умножают на самый большой из его простых делителей. Из скольких чисел в результате нескольких таких операций можно получить 1875 = 3 ⋅ 54 ?
Задача 4.
По кругу сидело пять человек, каждый из которых был рыцарем или лжецом. Известно также, что было хотя бы по одному человеку обоих типов. Каждому из сидящих за столом задали вопрос: «Сколько среди двух твоих соседей рыцарей?» На этот вопрос не были даны никакие ответы, кроме, возможно, «Два» и «Ноль». Сколько рыцарей могло сидеть в круге?
Задача 5.
Можно ли фигуру на рисунке разбить на квадраты и треугольники, как на рисунке справа?
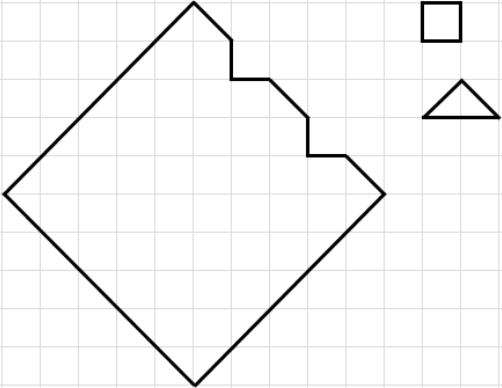
Задача 6.
Из 10 различных цифр составлены 4 числа. Самое большое из них составлено из самых маленьких цифр, а самое маленькое число делится на 17. Найдите сумму двух средних чисел.
Задача 7.
На доске написано число 321321321321. Какие цифры нужно стереть, чтобы получить наибольшее возможное число, которое делится на 36?
Задача 8.
Клетки доски 7 × 7 окрашены в шахматном порядке так, что углы окрашены в чёрный цвет. Разрешается перекрашивать в противоположный цвет любой уголок из трёх клеток. Можно ли с помощью таких операций перекрасить всю доску в белый цвет?

