Задача 1.
К следователю привели шестерых обвиняемых, из которых ровно трое — преступники, и семерых свидетелей, из которых ровно трое — лжесвидетели. Лжесвидетели всегда говорят неправду, а остальные говорят правду. Знающий всё вышеописанное следователь может спросить у любого свидетеля про любого обвиняемого: «Это преступник?» Как следователю найти всех преступников, задав не более 11 вопросов?
Задача 2.
Антон и Боря играют в игру, делая ходы по очереди, начинает Антон. Изначально у них была пустая клетчатая доска размером 5 × 5. Каждым ходом можно поставить любое натуральное число в любую свободную клетку. Когда пустых клеток не остаётся, игроки считают произведения всех чисел в каждой строке, каждом столбце и на двух главных диагоналях. Боря объявляется победителем, если все 12 произведений чётны, иначе выигрывает Антон. Кто может выиграть при любой игре соперника?
Задача 3.
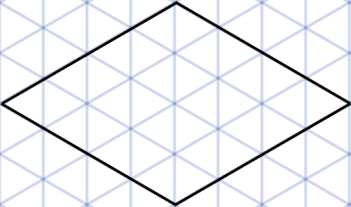
Варя нарисовала на треугольной сетке ромб площадью 32 маленьких треугольника (см. рисунок). Гоша хочет разрезать этот ромб по линиям сетки на две фигуры так, чтобы периметры у фигур были равными, а площади отличались как можно больше. Какую наибольшую разницу площадей сможет получить Гоша?
Задача 4.
На птичьем базаре продают птиц. Известно, что более 1/7 всех птиц составляют страусы, более 1/3 всех птиц – голуби и более 1/2 всех птиц – попугаи. Какое наименьшее количество птиц может продаваться на базаре?
Задача 5.
В какое наибольшее количество цветов можно раскрасить клетки прямоугольника 2 × 8 так, чтобы каждая клетка имела соседей по стороне ровно двух цветов?
Задача 6.
Решите числовой ребус: СИЛА + МУЛ ⋅ 6 = МУЛАТ. Разные буквы обозначают разные цифры, а одинаковые буквы – одинаковые цифры.

