Задача 1.
Карлсон пришёл в магазин закупиться вареньем. Банка малинового варенья стоила 115 рублей, банка вишнёвого — 175 рублей, а банка клюквенного — 195 рублей. Известно, что Карлсон купил 100 банок варенья, при этом малинового и вишнёвого варенья было куплено поровну, а всего Карлсон заплатил за покупку 16 тысяч рублей. Сколько варенья каждого вида купил Карлсон?
Задача 2.
К следователю привели шестерых обвиняемых, из которых ровно трое — преступники, и семерых свидетелей, из которых ровно трое — лжесвидетели. Лжесвидетели всегда говорят неправду, а остальные говорят правду. Знающий всё вышеописанное следователь может спросить у любого свидетеля про любого обвиняемого: «Это преступник?» Как следователю найти всех преступников, задав не более 11 вопросов?
Задача 3.
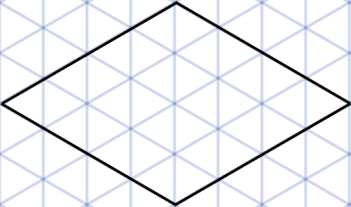
Варя нарисовала на треугольной сетке ромб площадью 32 маленьких треугольника (см. рисунок). Гоша хочет разрезать этот ромб по линиям сетки на две фигуры так, чтобы периметры у фигур были равными, а площади отличались как можно больше. Какую наибольшую разницу площадей сможет получить Гоша?
Задача 4.
На птичьем базаре продают птиц. Известно, что более 2/5 всех птиц – голуби, а более 4/7 всех птиц – попугаи. Какое наименьшее количество птиц может продаваться на базаре?
Задача 5.
В некоторый момент в Стамбуле до полудня оставалось вчетверо меньше времени, чем в Бомбее. А через четыре с половиной часа уже в Бомбее до полудня оставалось вчетверо меньше времени, чем в Стамбуле. Определите разницу во времени между Стамбулом и Бомбеем.
Задача 6.
Пётр Тормоз вышел на прогулку из пункта 𝐴 в пункт 𝐵 со скоростью 2 км/ч. Через 5 минут после этого вслед за ним из пункта 𝐴 вышел Иван Скороход со скоростью 9 км/ч, а из пункта 𝐵 навстречу ему – его брат Фёдор Скороход с такой же скоростью. Каждый раз, доходя до пунктов 𝐴 и 𝐵, братья сразу поворачивали и шли назад. Это продолжалось до тех пор, пока Пётр не пришёл в пункт 𝐵. Кто из братьев чаще оказывался с Петром в одной точке, если расстояние между 𝐴 и 𝐵 не меньше 10 км?
Задача 7.
На доске написаны пять различных натуральных чисел. Для каждой пары чисел на доске Саша посчитал НОК и записал себе в тетрадь, а Вася посчитал НОК для каждых трёх чисел на доске и записал себе в тетрадь. Могло ли случиться так, что в тетрадях у Саши и Васи написаны одинаковые наборы чисел?
Задача 8.
Коля нарисовал связную фигуру из восьми клеток. Люда увидела фигуру и сказала, что внутри фигуры можно ровно двумя способами выбрать квадратик 2 × 2. Чему может быть равен периметр Колиной фигуры?

