Задача 1.
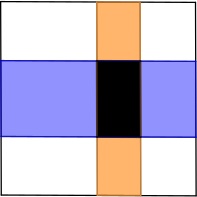
Два прямоугольника одинаковой площади, синий и оранжевый, расположены в большом прямоугольнике, как показано на рисунке. В пересечении синего и оранжевого прямоугольников получился прямоугольник, площадь которого в 100 раз меньше площади большого. А во сколько раз его периметр меньше периметра большого?
Задача 2.
Цветик-семидесятицветик имеет 30 красных и 40 зелёных лепестков. Лепестки можно срывать только парами. Если сорвать два красных лепестка, то вырастут красный и зелёный. Если сорвать два зелёных, то вырастет красный. А если сорвать красный и зелёный, то вырастут два зелёных. Девочка Женя 60 раз срывала по два лепестка, и красных лепестков совсем не осталось. А сколько осталось зелёных лепестков?
Задача 3.
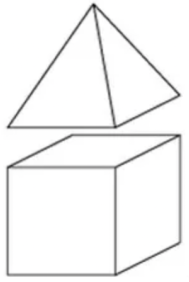
Матвей строит бассейн: по периметру прямоугольником он ставит на землю бетонные кубы вплотную друг к другу, а на некоторые из них сверху ещё ставит пирамидку (см. рисунок). Когда он с гордостью оглядел своё творение, он заметил, что у его бассейна 48 видимых граней (те грани, которые примыкают к земле или касаются друг друга, конечно, не видны). Чему могло быть равно общее количество использованных блоков (суммарное число кубов и пирамидок)?
Задача 4.
Незнайка взял стопку бумаги и сложил её пополам, получив тем самым стопку из нескольких вложенных друг в друга двойных листов. После этого он разрезал полученную стопку двумя прямыми разрезами, параллельными краям листов. Когда Незнайка развернул все сложенные части, у него получилось 60 прямоугольных кусочков. Сколько листов могло быть первоначально в стопке?
Задача 5.
На доске было написано натуральное число. Пришла Машенька, умножила его на 16 и записала вместо него. Прибежал Вовочка и стёр последнюю цифру. Пришла Настенька и умножила число на доске на 6. Вовочка снова стёр последнюю цифру. Могло ли после этого на доске оказаться первоначальное число?
Задача 6.
На доске написано пять натуральных чисел (среди них могут быть повторяющиеся). К доске подошли 10 детей и посмотрели на числа, после чего каждый ребёнок сделал заявление.
- Первый: «Среди чисел на доске есть два, произведение которых равно 1».
- Второй: «Среди чисел на доске есть два, произведение которых равно 2».
- …
- Десятый: «Среди чисел на доске есть два, произведение которых равно 10».
Какое наибольшее количество детей могли сказать правду?
Задача 7.
Арина продавала на блошином рынке алмазики, несколько штучек. Торговля не шла, и она снизила цену алмазика на 20 рублей. Продав по этой цене четыре штучки, она снизила цену ещё на 20 рублей. В результате она продала все алмазики и заработала столько же денег, сколько заработала бы, продав все алмазики на 32 рубля дешевле, чем планировала. Сколько алмазиков было у Арины?
Задача 8.
У Никиты имеется пять гирь, массы которых равны 1 г, 2 г, 3 г, 4 г, 5 г. К сожалению, массы гирь не подписаны. Как за три взвешивания на чашечных весах определить чётность массы в граммах хотя бы какой-нибудь гири?

