Задача 1.
В коробке лежат 10 красных шариков, 20 синих и 30 зелёных. Серёжа вытаскивает шарики, пока у него не окажется разное количество шариков каждого из трёх цветов (изначально считается, что у него одинаковое количество шариков каждого цвета: их нет). Какое наибольшее количество шариков может вытащить Серёжа?
Задача 2.
На бесконечном клетчатом поле в клетке с координатами (0; 0) сидит лягушка, которая умеет прыгать на соседнюю клетку (в том числе по диагонали). Сколькими способами она может добраться за шесть прыжков до клетки с координатами (6; 4)?
Задача 3.
Таблица из 11 строк и 100 столбцов заполнена числами — по одному числу в клетке. Известно, что в каждой строке, кроме последней, есть хотя бы 91 число, которое больше, чем число под ним (в том же столбце следующей строки). Может ли в последней строке найтись 91 число, которое больше, чем число в том же столбце в первой строке?
Задача 4.
В строчку выписали без пробелов натуральные числа, начиная с 2024: 202420252026 . . . В какой-то момент в этой строке впервые встретился кусок «2023». Какие три цифры идут после него?
Задача 5.
В любой группе из трёх приехавших в лагерь школьников либо все трое попарно знакомы (то есть все знают всех), либо знакома только одна пара людей (а третий человек людей из пары не знает). По приезде в лагерь у Андрея оказалось 50 друзей, а у Бориса – 40. Сколько школьников приехало в лагерь?
Задача 6.
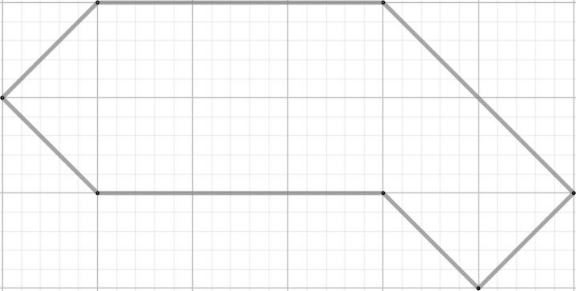
Докажите, что фигуру на рисунке можно разрезать на любое чётное количество равных кусочков.
Задача 7.
В начале урока учитель спросил детей «В смысле?» и получил ответы: «В прямом», «В переносном», «В коромысле». В конце урока он задал тот же вопрос и получил тот же набор ответов. Оказалось, что тех, кто хотя бы раз ответил «В коромысле», и тех, кто так не отвечал, поровну. Ответивших хотя бы раз «В прямом» оказалось вдвое больше тех, кто ни разу так не отвечал. И, наконец, тех, кто ответил «В переносном», было в три раза больше, чем тех, кто так не отвечал. Во сколько раз меньше ответивших одинаково по сравнению с теми, кто поменял свой ответ?
Задача 8.
На острове живёт два племени: рыцари и лжецы (рыцари всегда говорят правду, лжецы всегда врут). Однажды там построили отель, как на рисунке. Он поделён на двухклеточные номера, в каждой клетке которого живёт человек. Каждый житель чёрной клетки сказал: «Мой сосед по номеру — человек из другого племени», а каждый житель белой клетки сказал: «Мой сосед по номеру — человек из моего племени». Сколько рыцарей может жить в отеле?


