Задача 1.
Числа 1, 2, . . . , 64 расставлены в каком-то порядке на доске 8 × 8. Докажите, что можно указать хотя бы четыре квадрата 2 × 2, сумма чисел в каждом из которых больше 100.
Задача 2.
По кругу сидело пять человек, каждый из которых был рыцарем или лжецом. Известно также, что было хотя бы по одному человеку обоих типов. Каждому из сидящих за столом задали вопрос: «Сколько среди двух твоих соседей рыцарей?» На этот вопрос не были даны никакие ответы, кроме, возможно, «Два» и «Ноль». Сколько рыцарей могло сидеть в круге?
Задача 3.
Имеется несколько доминошек трёх типов: каждая покрашена в два из трёх имеющихся цветов — всего три разных вида. Доминошки выложены в замкнутую цепочку по правилам игры домино. Может ли так случиться, что количества доминошек каждого типа являются трёмя последовательными числами?
Задача 4.
Можно ли фигуру на рисунке разбить на квадраты и треугольники, как на рисунке справа?
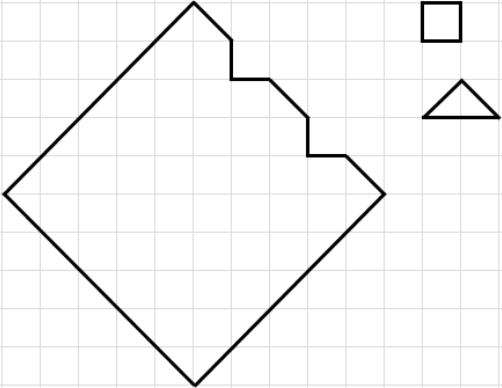
Задача 5.
На доске написано число 321321321321. Какие цифры нужно стереть, чтобы получить наибольшее возможное число, которое делится на 36?
Задача 6.
Четыре прямых проведены так, что никакие две из них не параллельны и никакие три не пересекаются в одной точке. Они разделили плоскость на 11 частей. Можно ли расставить в эти части натуральные числа от 1 до 11 (каждое — один раз) так, чтобы для каждой прямой суммы чисел по разные стороны от неё были равными?
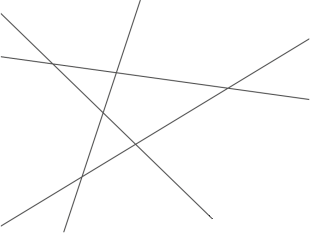
Задача 7.
Серёжа хочет замостить плиткой квадрат 6 × 6. У него есть 36 одинаковых плиток 1 × 1 с узором как на левом рисунке — отрезки соединяют середины сторон плитки. При укладке плитку можно поворачивать. Когда плитки будут уложены, эти отрезки образуют несколько путей (возможно, замкнутых). Какое наименьшее число путей может образоваться? Например, на правом рисунке в квадрате 4 × 4 образовалось девять путей.
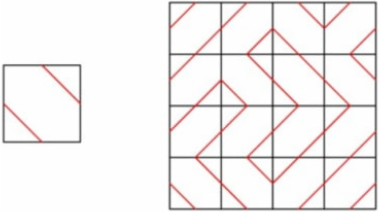
Задача 8.
Каждый день, когда Миша приходит в школу, он получает 1 двойку, 2 тройки, 5 четвёрок и 10 пятёрок. Каждый день, когда Маша приходит в школу, она получает 5 двоек, 2 тройки, 7 четвёрок и 16 пятёрок. Известно, что Миша и Маша несколько раз сходили в школу и получили поровну четвёрок, а также 3000 пятёрок. Сколько всего двоек, троек и четвёрок получил каждый из ребят? (Миша и Маша могут прогуливать школу в разные дни.)

