Задача 1.
В коробке лежат 10 красных шариков, 20 синих, 30 зелёных и 40 белых. Серёжа вытаскивает шарики, пока у него не окажется разное количество шариков каждого из четырёх цветов (изначально считается, что у него одинаковое количество шариков каждого цвета: их нет). Какое наибольшее количество шариков может вытащить Серёжа?
Задача 2.
На бесконечном клетчатом поле в клетке с координатами (0; 0) сидит лягушка, которая умеет прыгать на соседнюю клетку (в том числе по диагонали). Сколькими способами она может добраться за шесть прыжков до клетки с координатами (6; 3)?
Задача 3.
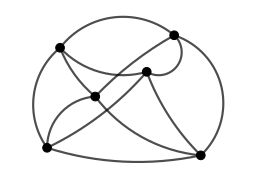
В стране гномов шесть городов, которые соединены дорогами так, как показано на рисунке. Всё было хорошо, но на города стал нападать дракон. Дракон разрушает все дороги, идущие из выбранного города, но трудолюбивые гномы сразу же строят дороги из этого города во все города, с которыми он не был соединён прямо перед этим. Дракон хочет, чтобы страна разделилась на четыре не соединённых друг с другом региона. Сможет ли он это сделать?
Задача 4.
Равносторонний треугольник со стороной 4 разбит на 16 равносторонних треугольников со стороной 1. Некоторые треугольники покрашены белым цветом, остальные – чёрным. За один ход можно перекрасить в противоположный цвет любой треугольник и все соседние с ним по стороне. Верно ли, что из любой исходной позиции можно сделать все треугольники белыми?

