Задача 1.
С натуральным числом проделывают следующую операцию: его делят на самый маленький из его простых делителей и одновременно умножают на самый большой из его простых делителей. Из скольких чисел в результате нескольких таких операций можно получить 1875 = 3 ⋅ 54 ?
Задача 2.
На площади стоят 100 столбов, каждые два соединены ровно одним проводом. Электрик Петров покрасил провода в красный и зелёный цвета. После этого счетовод Сидоров на каждом красном проводе написал, сколько зелёных проводов имеют с ним общий конец. Может ли сумма всех написанных чисел равняться 233333?
Задача 3.
Невидимый заяц сидит в одной из вершин 14-угольника. Услышав выстрел, он перебегает в соседнюю вершину. Три охотника находятся в центре этого 14-угольника, откуда зайца не видно, поэтому стреляют наугад по вершинам (поражают по три вершины за каждый выстрел, причём не промахиваются — если заяц находится в вершине, то он считается убитым). Покажите, как охотники смогут гарантированно убить зайца не более чем за шесть выстрелов.
Задача 4.
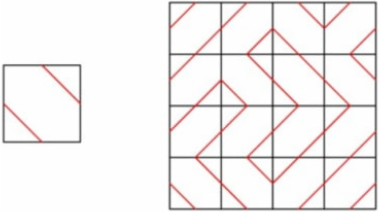
Серёжа хочет замостить плиткой квадрат 20 × 20. У него есть 400 одинаковых плиток 1 × 1 с узором как на левом рисунке — отрезки соединяют середины сторон плитки. При укладке плитку можно поворачивать. Когда плитки будут уложены, эти отрезки образуют несколько путей (возможно, замкнутых). Какое наименьшее число путей может образоваться? Например, на правом рисунке в квадрате 4 × 4 образовалось девять путей.