Задача 1.
Четыре нимфы встретили 8 фей. У фей не было цветов, и поэтому каждая нимфа подарила каждой фее по 5 цветов. После этого у каждой феи и у каждой нимфы стало одинаковое количество цветов. Сколько цветов изначально было у каждой нимфы?
Задача 2.
В некотором уезде живут купцы и разбойники. Купцы всегда говорят правду, а разбойники всегда лгут. Однажды на лугу собралась компания из 8 жителей. Оказалось, что у каждого из них в этой компании имеется ровно один знакомый. На вопрос «Твой знакомый купец или разбойник?» каждый ответил: «Мой знакомый – разбойник!» Сколько купцов и сколько разбойников в этой компании?
Задача 3.
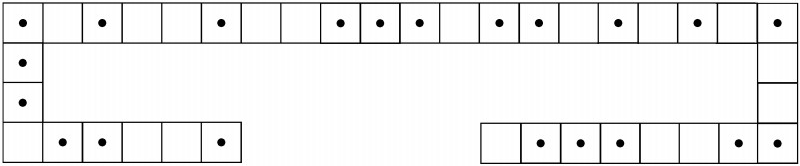
Разделите по линиям сетки фигуру на 6 равных по форме и по размеру частей.

Задача 4.
Паук Ефим живёт в сарае у Пахома, который очень боится пауков. Однажды Пахом посадил прямо под паутиной Ефима дергун-траву с двумя зубастиками. Каждое утро зубастик перемещается на 3 сантиметра вверх, если паук над зубастиком, или на 3 сантиметра вниз, если паук под зубастиком. Каждый вечер Ефим перемещается на 1 или 2 сантиметра вверх или вниз. Оказавшись на одном уровне с зубастиком, паук попадает ему в зубы. Сможет ли Ефим добраться до пола сарая, если сейчас он на потолке (высотой 210 сантиметров), а первый зубастик — на высоте 1 сантиметр над землёй, второй зубастик — 4 см над землёй?
Задача 5.
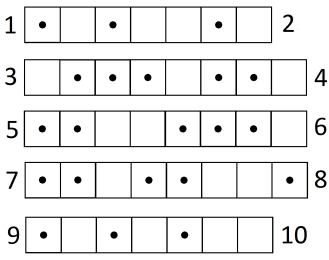
Ефим разрезал ленту (на рисунке снизу лента изображена в свёрнутом виде) на части (второй рисунок снизу). Запиши, в каком порядке надо склеить получившиеся части, чтобы восстановить ленту.
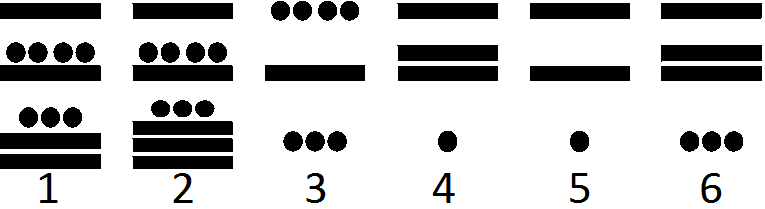
Задача 6.
Для записи чисел индейцы племени майя разработали особую систему, которая, среди прочего, использовалась в их календарях. Года 1703, 2101, 2193, 2198, 2201 и 2203 записаны ниже в этой системе в неизвестном порядке. Укажите, где какой год.