Задача 1.
Археологи при раскопках древнего Новгорода нашли кусок бересты XI века с расчётами зодчего Истомы (рисунок ниже), в которых частично использована древнерусская система записи чисел. Помогите им записать все равенства арабскими цифрами.
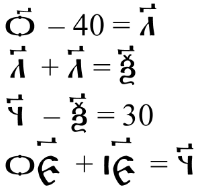
Задача 2.
Косая сажень да маховая сажень вместе намного длиннее, чем аршин да пядь вместе. Но если взять косую сажень да пядь, то вместе они будут лишь немного длиннее, чем маховая сажень да аршин. А уж маховая сажень да аршин вместе и вовсе равны косой сажени да пяди вместе. Запиши эти меры длины в порядке возрастания.
Задача 3.
Три купца вместе пожертвовали 91 монету.
- Первый купец сказал: «Я дал столько, сколько было бы всего денег, если бы я дал во столько же раз меньше, во сколько раз больше денег дал я, чем второй».
- Второй купец: «Я дал денег во столько же раз меньше, чем третий, во сколько раз третий дал бы больше, чем дали бы мы вдвоём с первым вместе, если бы третий дал в пять раз больше».
Сколько монет дал каждый купец?
Задача 4.
Механик изготовил хронометр, показывающий время в мигах и мгновениях. В обычных сутках 6 мигов, в миге 15 мгновений. Сколько времени будет на этом хронометре, когда обычные часы показывают:
- 9:20
- 22:40
- время через два часа после 22:40 ?
Задача 5.
Древние племена использовали руны – буквы из четырёх одинаковых отрезков. Чтобы получить руну, нужно обвести четыре отрезка из показанных на картинке ниже.
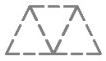
Слог составляется из двух рун, вторая из которых переворачивается и приписывается к первой снизу, например:

Нарисуйте как можно больше разных слогов, содержащих два треугольника, не имеющих общей стороны. Слоги, получающиеся друг из друга поворотом или отражением, считаются одинаковыми.
Задача 6.
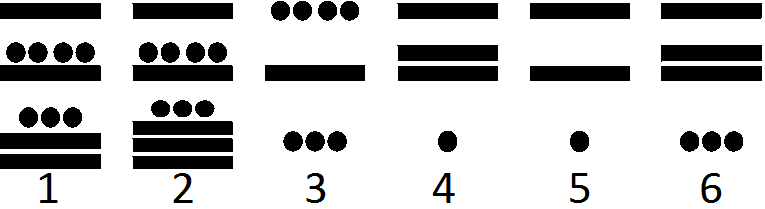
Для записи чисел индейцы племени майя разработали особую систему, которая, среди прочего, использовалась в их календарях. Года 1703, 2101, 2193, 2198, 2201 и 2203 записаны ниже в этой системе в неизвестном порядке. Укажите, где какой год.