Олимпиада «Осенний Олимп», 4 класс, 2015 год, 1 тур
дата проведения: 23 сентября 2015
Задача 3.
Во все клетки квадрата, кроме центральной, Ефим вписал все целые числа от 0 до 7 так, чтобы сумма чисел вдоль каждой стороны квадрата была равна 9. Чему может быть равна сумма чисел в клетках с номерами 2, 4, 6, 8?
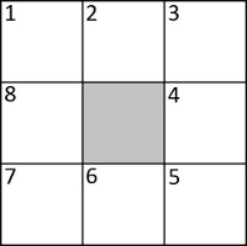
Ответ на Задачу 3.
Ответ: 20.
Решение:
Сумма всех чисел от 0 до 7 равна 28. Суммы чисел вдоль верхней и нижней сторон равны 9, значит, сумма чисел в 8 и 4 клетках равна 28 − 9 − 9 = 10. Суммы чисел вдоль правой и левой сторон равны 9, значит, сумма чисел во 2 и 6 клетках равна 28 − 9 − 9 = 10. Получается, что сумма чисел в клетках с номерами 2, 4, 6, 8 равна 10 + 10 = 20

