Задача 1.
У Святослава на столе стоят электронные часы, а рядом с ними два зеркала: одно стоит справа от часов, а другое лежит перед ними. Посмотрев на часы, Святослав обнаружил, что число минут в два раза больше числа часов. При этом третья цифра на часах в обоих зеркалах не изменилась; вторая цифра, отраженная в нижнем зеркале, превратилась в другую цифру; а четвёртая цифра в обоих зеркалах превратилась в бессмыслицу. Какое время показывают часы Святослава? (Образцы цифр приведены на рисунке).
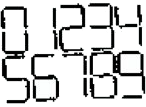
Задача 2.
В трактир зашли три мудреца. Известно, что, если мудрецу известен ответ на вопрос, то он скажет правду, а если нет, то скажет, что не знает ответа. Трактирщик задал им вопрос: «Сколько из вас хотят пить?»
- Первый мудрец: «Не знаю, сколько, но знаю, что хотя бы двое».
- Второй мудрец: «Не знаю».
- Третий мудрец: «Двое».
Кто из мудрецов хочет пить?
Задача 3.
Некоторую сумму денег нужно распределить между трёмя братьями так, чтобы первый получил на 200 рублей меньше половины всей суммы, второй — на 300 рублей меньше трети, а третий — на 100 рублей меньше четверти всей суммы. Какова величина всей суммы, и сколько получит каждый?
Задача 4.
У Пика есть многоугольный лист бумаги очень больших размеров. Сначала он нарисовал на каждой стороне этого листа квадратик так, что одна из сторон квадратика лежит на этой стороне, но ни одна из его вершин не совпадает с вершиной листа. После этого Пик вырезал все нарисованные квадратики, и лист не распался на части (возможный результат таких действии Пика показан на рисунке на примере шестиугольника). Известно, что площадь каждого вырезанного квадратика равна 36 см2‚ а периметр листа увеличился на 312 сантиметров. Сколько сторон было у многоугольного листа изначально?

Задача 5.
Злой Колдун взял в плен нескольких Принцесс и нескольких Драконов и рассадил их в свои секретные тюрьмы с квадратными камерами, по одному пленнику в каждую камеру. Принцессы всегда говорят правду, а Драконы всегда лгут. Пленники видели своих соседей через окошко в стене (соседними считаются камеры, имеющие общую стенку). Однажды каждый пленник сказал: «Среди моих соседей Принцесс столько же, сколько и Драконов». Сколько Принцесс могло быть в этой тюрьме злого Колдуна? (см. рисунок)

Задача 6.
На берегу реки, скорость течения которой 10 м/с, стоит избушка, в 225 метрах от которой ниже по течению привязан первый плот, а в 125 метрах выше по течению — второй. Из избушки сначала выбегает заяц и с постоянной скоростью бежит к первому плоту, а через 10 с после этого — Дед Мазай, но бежит он ко второму плоту со скоростью 5 м/с, запрыгивает на него и тут же отчаливает. С какой наименьшей целочисленной скоростью (6 м/с) должен бежать заяц, чтобы, когда он добежит до плота, Дед Мазай ещё находился бы выше по течению?

