Задача 1.
Рабочая лошадь за 15 минут может пройти 600 саженей, а вол за 25 минут может пройти 500 саженей. Во сколько раз рабочая лошадь передвигается быстрее, чем вол?
Комментарий: Сажень – старинная русская мера длины.
Задача 2.
Некий помещик купил несколько десятин пахоты по 120 рублей за десятину и несколько десятин леса по 200 рублей за десятину. Всего он купил 60 десятин земли, уплатив при этом 5120 рублей. Сколько было куплено пахоты, а сколько леса?
Комментарий: Десятина – старинная русская единица земельной площади.
Задача 3.
На поляну пришли лось, заяц, волк, медведь, енот. Все звери встали в ряд. Сначала каждый, кто стоял на втором и на четвёртом месте, в том же порядке (сначала второй, потом четвёртый) встали в конец строя. Потом опять каждый, кто теперь стоял на первом, третьем, пятом месте, в том же порядке встали в конец строя. Оказалось, что теперь звери стоят в таком порядке: енот, заяц, волк, медведь, лось. Напишите, кто на каком месте стоял первоначально.
Задача 4.
На именины Добрыни испекли два одинаковых прямоугольных пирога с ягодками и полосками варенья:
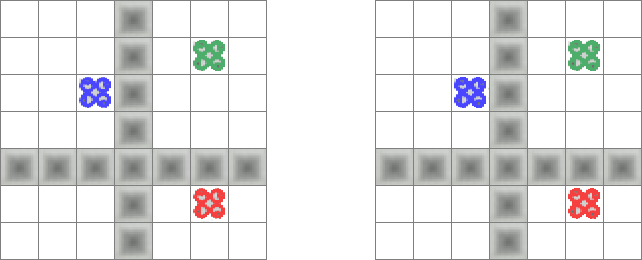
Добрыня разрезал один из пирогов по линиям сетки на 2 части (не обязательно прямолинейным разрезом) и сложил эти части вместе. Его сестра Агриппина разрезала второй пирог на 2 части и сложила его части вместе. Получились такие пироги:

Покажите линии разреза пирогов Добрыни и Агриппины.
Задача 5.
У Бабы Яги есть волшебные сундуки (вид сверху):
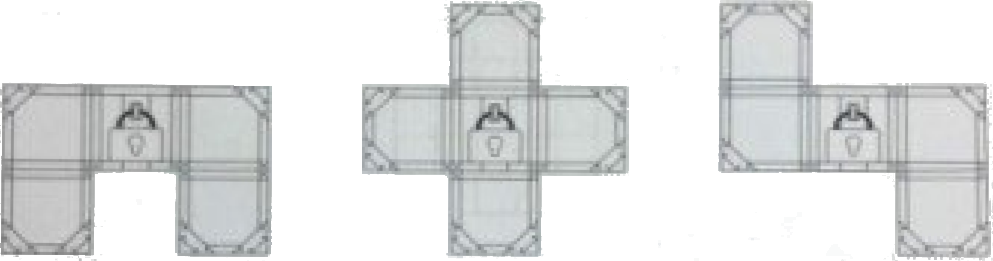
Нарисуйте по клеточкам плащ-невидимку, под которым можно спрятать любой сундук. Используйте как можно меньше клеточек. Чтобы спрятать сундук, надо накрыть плащом его крышку.
Задача 6.
На столе лежит вот такая бумажная таблица:

Степан разложил несколько ключиков в клетки этой таблицы. Ефим берёт 6 вот таких полосок (он их не поворачивает):
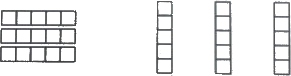
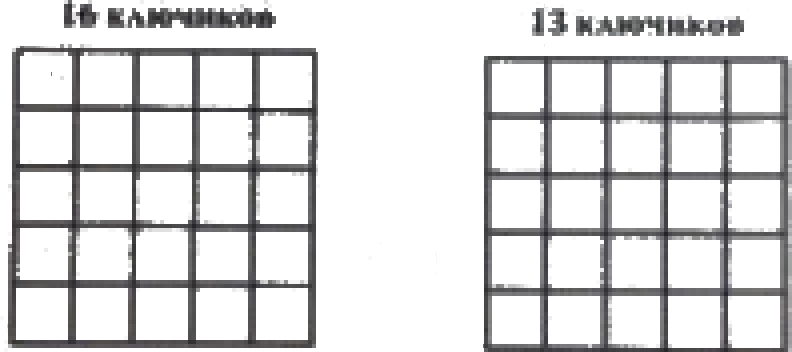
Как бы Ефим их ни положил в таблицу, хотя бы один ключик всегда видно. На левом рисунке покажите, как Степан разложил ключики, если у него их 16. На правом рисунке покажите, как Степан сделал это, если у него их 13.
Задача 7.
Рабочий выложил бесконечную мозаику из одинаковых квадратов. Фрагмент мозаики представлен на рисунке ниже:

Раскрасьте квадраты в три цвета так, чтобы выполнялись два условия (вместо раскраски вы можете просто расставить в квадратах цифры 1, 2, 3):
- квадраты одинакового цвета могут граничить только по вершине (или не граничить вообще);
- если убрать все квадраты любого цвета, то из любого квадрата одного из оставшихся цветов можно будет попасть в любой оставшийся квадрат, переходя в соседний через сторону или, может быть, её часть (но не через вершину).

