Задача 1.
Джинн научил Али Бабу арифметике джиннов, в которой все действия выполняются по очереди, слева направо. Известно, что:
- ХАЛВА ⊙ ХАЛВА = ЛУКУМ
- ЛУКУМ ⊙ ХАЛВА = ХАЛВА
- ХАЛВА ⊙ ЛУКУМ = ХАЛВА
- ЛУКУМ ⊙ ЛУКУМ = ХАЛВА
- ХАЛВА ⊕ ХАЛВА = ХАЛВА
- ЛУКУМ ⊕ ХАЛВА = ЛУКУМ
- ХАЛВА ⊕ ЛУКУМ = ЛУКУМ
- ЛУКУМ ⊕ ЛУКУМ = ЛУКУМ
Заполните пропуски так, чтобы равенство стало верным:
ХАЛВА ⊙ _____ ⊕ _____ ⊙ _____ ⊕ ХАЛВА = ЛУКУМ
Задача 2.
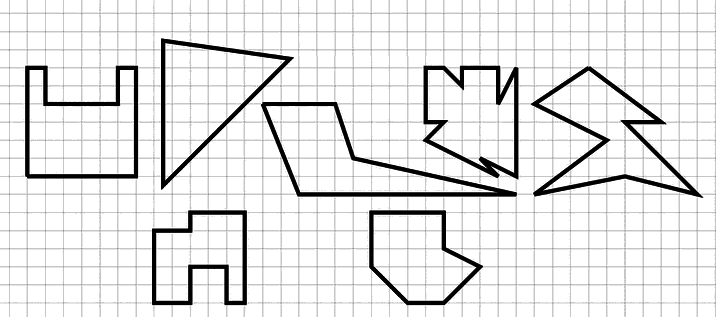
Торговец необычными украшениями хочет вставить драгоценный камень в одну из своих оправ (края камня не должны вылезать за пределы оправы; камень можно переворачивать и поворачивать на прямой угол).

В какие оправы может поместиться данный камень?
Задача 3.
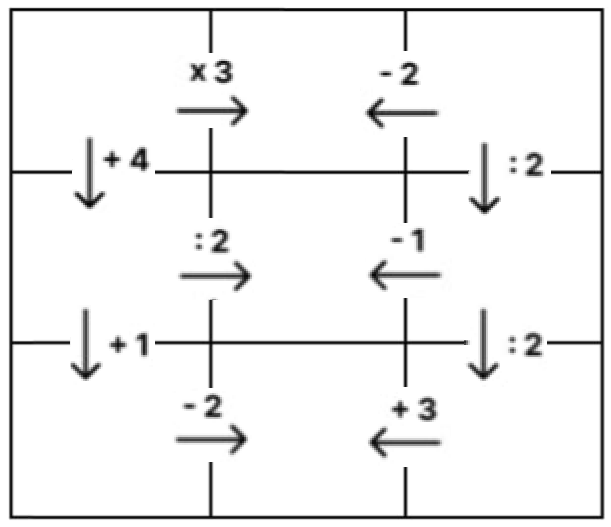
Чтобы проникнуть в древнюю сокровищницу, Али Бабе необходимо вписать в клетки однозначные числа, полностью заполнив таблицу. Между клетками указано, какую операцию нужно применить к числу, чтобы получить соседнюю. Операции выполняются по направлению стрелок. Помогите Али Бабе заполнить таблицу!
Задача 4.
Абдулла куёт кольчужные перчатки.
- Если заказать у него от 1 до 40 перчаток, возьмёт он по 5 дирхамов за перчатку.
- Если заказать у него от 41 до 80 перчаток, возьмёт он по 4 дирхама за перчатку.
- Если заказать у него не менее 81 перчаток, возьмёт он по 3 дирхама за перчатку.
Али Баба тоже куёт кольчужные перчатки. По умолчанию он берёт 5 дирхамов за перчатку, но если сделать заказ у Абдуллы, а потом — у Али Бабы, то Али Баба готов за каждую перчатку брать на 1 дирхам меньше, чем взял Абдулла.
Например, если заказать у Абдуллы 50 перчаток, а у Али Бабы — 60, то возьмут они суммарно (50 × 4 + 60 × 3) дирхамов.
Султан хочет снарядить перчатками 35 стражников, заказав их часть (возможно, пустую) у Абдуллы, а часть (возможно, пустую) — у Али Бабы. Какое наименьшее количество дирхамов он может потратить для этого? Одному стражнику нужны 2 перчатки!
Задача 5.
В сундуке визиря было 120 фунтов драгоценностей. Злой ифрит украл половину драгоценностей, а коварный ракшас украл половину оставшихся. А чтобы визирь ничего не заметил, каждый из них клал вместо украденных драгоценностей пустые шкатулки (вес сундука при этом сохранялся). Такая шкатулка с 5 фунтами драгоценностей весит столько же, сколько 3 шкатулки, каждая — с фунтом драгоценностей. Сколько шкатулок в итоге оказалось в сундуке?
Задача 6.
Учёные Абу, Джафар и Надим писали научные книги. Каждый смог написать хотя бы 2 книги, но меньше, чем 12 книг. Все написанные книги отнесли в библиотеку и заметили, что:
- Абу написал аж 7 книг.
- Надим написал меньше книг, чем Абу.
- Джафар с Надимом в сумме написали книг больше, чем Абу.
Отметьте заведомо истинные высказывания:
- Всего написано 14 книг
- Всего Абу, Джафар и Надим могли написать ровно 22 книги
- Джафар написал ровно 4 книги, а Надим — ровно 2 книги
- Надим мог написать ровно 9 книг
- Всего Абу, Джафар и Надим могли написать ровно 16 книг
Должны быть отмечены все заведомо истинные высказывания и не отмечено ни одного, которое может быть ложным.

