Задача 1.
Джинн научил Али Бабу арифметике джиннов, в которой все действия (если не стоят скобки) выполняются по очереди, слева направо. Известно, что:
- ХАЛВА ⊙ ХАЛВА = ХАЛВА
- ЛУКУМ ⊙ ХАЛВА = ХАЛВА
- ХАЛВА ⊙ ЛУКУМ = ЛУКУМ
- ЛУКУМ ⊙ ЛУКУМ = ХАЛВА
- ХАЛВА ⊕ ХАЛВА = ХАЛВА
- ЛУКУМ ⊕ ХАЛВА = ХАЛВА
- ХАЛВА ⊕ ЛУКУМ = ХАЛВА
- ЛУКУМ ⊕ ЛУКУМ = ЛУКУМ
Заполните пропуски так, чтобы равенство стало верным:
ХАЛВА ⊙ _____ ⊕ ( _____ ⊙ _____ ) ⊕ ЛУКУМ = ЛУКУМ
Задача 2.
Чтобы магические ворота открылись, Али Бабе нужно вставить в замок некоторые камни:
- их можно поворачивать на прямой угол и переворачивать
- клетки камней должны лежать строго на клетках замка
- камни не должны выходить за границы замка и накладываться друг на друга
Камни нужно вставить так, чтобы число не закрытых камнями клеток замка оказалось наименьшим возможным. Чему равно это число?
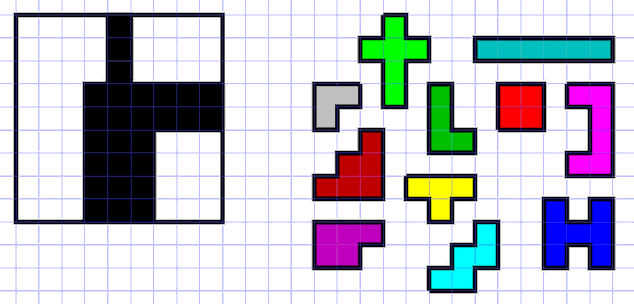
На рисунке замок изображён слева, полный набор камней — справа. Чёрным цветом на замке помечена область, на которую ставить камни нельзя.
Задача 3.
Джинн загадал султану трёхзначное число. В этом числе:
- Первая цифра меньше второй в 2 раза
- Третья цифра является суммой первой и второй цифр и единицы
- Если же умножить загаданное число на 2, то первая цифра станет совпадать с третьей
Какое число могло быть загадано? Укажи все варианты.
Задача 4.
Отряд из 13 всадников хочет купить себе новые мечи и луки. Рашид, изготавливающий мечи, говорит, что первый меч он продаст за 3 дирхама, но каждый следующий меч будет стоить на 1 дирхам дороже предыдущего. Фатим, делающий луки, говорит, что лук стоит 6 дирхамов, но каждый второй лук он продаст за полцены. Каждому всаднику требуется меч или лук. Какое наименьшее количество дирхамов может потратить отряд?
Задача 5.
В одном риале 100 дирхамов. У Синбада-морехода ровно 475 риала. Мешок со специями стоит 20 риалов и 50 дирхамов. За каждый купленный мешок Синбаду на следующий день возвращают 1 риал 50 дирхамов.
Какое наибольшее число мешков сможет купить Синбад? Синбад готов тратить свои исходные 475 реалов, а также те деньги, которые ему будут возвращать за купленные мешки.
Задача 6.
Учёные Абу, Джафар и Надим писали научные книги. Каждый смог написать хотя бы 2 книги, но меньше, чем 8 книг. Все написанные книги отнесли в библиотеку и заметили, что:
- Абу написал не менее 4 книг.
- Джафар с Надимом в сумме написали книг меньше, чем Абу.
- Все трое учёных написали различные количества книг.
Отметьте заведомо истинные высказывания:
- Всего Абу, Джафар и Надим написали не менее 8 книг
- Всего Абу, Джафар и Надим написали не менее 9 книг
- Всего Абу, Джафар и Надим написали не менее 10 книг
- Абу мог написать ровно 4 книги
- Абу мог написать ровно 5 книг
- Абу мог написать ровно 6 книг
- Если Абу написал ровно 6 книги, то Джафар с Надимом написали ровно 5 книг
- Если Джафар написал ровно 3 книги, то Надим написал ровно 2 книги
- Если Джафар с Надимом написали ровно 5 книг, то Абу написал ровно 6 книг
Нужно отметить все заведомо истинные высказывания и не отметить ни одного, которое может быть ложным.
Задача 7.
Встретились пираты Умо, Амо, Мо, Джо и ещё один, имени которого мы не знаем. Каждый из пиратов сказал ровно одну фразу. Вот эти фразы (в каком-то порядке):
- В моём имени меньше букв, чем в любом из ваших!
- Первая буква моего имени идёт в русском алфавите раньше любой из первых букв ваших имён!
- Первая буква моего имени такая же, как первая буква имени одного из вас!
- Меня зовут так же, как одного из вас!
- Меня зовут Джо, и у меня есть огромный зелёный попугай!
Всё это — чистая правда. Как могли звать пятого пирата? Укажи все варианты.

