Задача 1.
Джинн научил Али Бабу арифметике джиннов, в которой все действия выполняются по очереди, слева направо. Известно, что:
- ХАЛВА ⊙ ХАЛВА = ХАЛВА
- ЛУКУМ ⊙ ХАЛВА = ЛУКУМ
- ХАЛВА ⊙ ЛУКУМ = ЛУКУМ
- ЛУКУМ ⊙ ЛУКУМ = ЛУКУМ
- ХАЛВА ⊕ ХАЛВА = ХАЛВА
- ЛУКУМ ⊕ ХАЛВА = ЛУКУМ
- ХАЛВА ⊕ ЛУКУМ = ХАЛВА
- ЛУКУМ ⊕ ЛУКУМ = ЛУКУМ
Заполните пропуски так, чтобы равенство стало верным (нужно найти все возможные варианты):
ХАЛВА ⊙ _____ ⊕ _____ ⊙ _____ ⊕ ЛУКУМ = ХАЛВА
Задача 2.
Абу купил несколько корзин сладостей. Если он продаст их все по 9 дирхамов за корзину, то получит 40 дирхамов прибыли. Если же он продаст их все по 4 дирхама за корзину, то убыток составит 20 дирхамов. Сколько корзин мог купить Абу? Нужно найти все возможные варианты!
Задача 3.
Пров купил на базаре 20 гирь: весами в 1 унцию, 2 унции, 3 унции, и так далее до 20 унций. Он разложил эти гири по сундукам, да так, что ни в одном из них не оказалось пары гирь, веса которых различаются вдвое. Какое наименьшее количество сундуков мог использовать Пров?
Задача 4.
Отряд из 13 всадников хочет купить себе новые мечи и луки. Рашид, изготавливающий мечи, говорит, что первый меч он продаст за 3 дирхама, но каждый следующий меч будет стоить на 1 дирхам дороже предыдущего. Фатим, делающий луки, говорит, что лук стоит 6 дирхамов, но каждый второй лук он продаст за полцены. Каждому всаднику требуется меч или лук. Какое наименьшее количество дирхамов может потратить отряд?
Задача 5.
Ефим складывал журавликов, через час к нему присоединился Фома, ещё через три часа Ефим забрал 400 и ушёл, Фома складывал ещё час, и когда он закончил, у него было 600. Сколько всего журавликов сложили Ефим и Фома, пока работали вместе?
Задача 6.
Робинзон после кораблекрушения оказался на берегу треугольного острова. Пройдя до другого берега, он повернул к третьему и далее продолжил в том же духе (переходя от третьего берега к первому, от первого — ко второму, от второго — к третьему), пока вновь не оказался в точке, с которой начал своё путешествие. Вот так путь выглядел сверху:
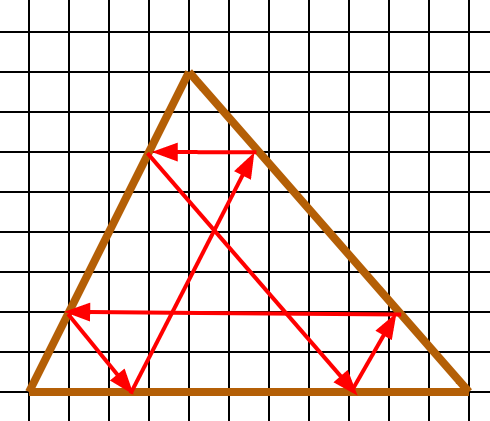
Путь состоит из участков, каждый из которых параллелен какому-то берегу. Его длина 1000 футов. Каков периметр острова?
Задача 7.
Встретились пираты Умо, Амо, Мо, Джо и ещё один, имени которого мы не знаем. Каждый из пиратов, за исключением одного, сказал ровно одну фразу. Вот эти фразы (в каком-то порядке):
- В моём имени меньше букв, чем в любом из ваших!
- Первая буква моего имени идёт в русском алфавите раньше любой из первых букв ваших имён!
- Первая буква моего имени такая же, как первая буква имени одного из вас!
- Меня зовут так же, как одного из вас!
Всё это — чистая правда. Как могли звать пятого пирата? Нужно найти все возможные варианты!

