Задача 1.
Джинн научил Али Бабу арифметике джиннов, в которой все действия выполняются по очереди, слева направо. Известно, что:
- ХАЛВА ⊙ ХАЛВА = ХАЛВА
- ЛУКУМ ⊙ ХАЛВА = ЛУКУМ
- ХАЛВА ⊙ ЛУКУМ = ЛУКУМ
- ЛУКУМ ⊙ ЛУКУМ = ЛУКУМ
- ХАЛВА ⊕ ХАЛВА = ХАЛВА
- ЛУКУМ ⊕ ХАЛВА = ЛУКУМ
- ХАЛВА ⊕ ЛУКУМ = ХАЛВА
- ЛУКУМ ⊕ ЛУКУМ = ЛУКУМ
Заполните пропуски так, чтобы равенство стало верным (нужно найти все возможные варианты):
ХАЛВА ⊙ _____ ⊕ _____ ⊙ _____ ⊕ ЛУКУМ = ХАЛВА
Задача 2.
Абу купил несколько корзин сладостей, заплатив за них суммарно целое количество дирхамов. Если он продаст их все по 9 дирхамов за корзину, то получит вдвое больше прибыли, чем убытка, который бы он получил, если бы продал их все по 4 дирхама за корзину. Какую наименьшую сумму Абу мог заплатить за корзины?
Задача 3.
Пров купил на базаре 200 гирь: весами в 1 унцию, 2 унции, 3 унции, и так далее до 100 унций, затем — 200 унций, 201 унцию, 202 унции и так далее до 299 унций. Он разложил эти гири по сундукам, да так, что ни в одном из них не оказалось пары гирь, веса которых различаются вдвое. Какое наименьшее количество сундуков мог использовать Пров?
Задача 4.
Отряд из 13 всадников хочет купить себе новые мечи и луки. Рашид, изготавливающий мечи, говорит, что первый меч он продаст за 3 дирхама, но каждый следующий меч будет стоить на 1 дирхам дороже предыдущего. Фатим, делающий луки, говорит, что лук стоит 6 дирхамов, но каждый второй лук он продаст за полцены. Каждому всаднику требуется меч или лук. Какое наименьшее количество дирхамов может потратить отряд?
Задача 5.
Ефим и Фома собирали бумажные журавлики. Каждый собирал журавлики со своей постоянной скоростью, и вместе они за 4 часа сложили 1000 журавликов. После этого Фома забрал 400 журавликов и ушёл. Ефим начал складывать журавлики с удвоенной скоростью и через ещё 4 часа перед ним опять было 1000 журавликов. Сколько журавликов собрал Фома?
Задача 6.
Робинзон после кораблекрушения оказался на берегу треугольного острова. Длина границы острова составляет 2000 футов. Пройдя до другого берега, он повернул к третьему и далее продолжил в том же духе (переходя от третьего берега к первому, от первого — ко второму, от второго — к третьему), пока вновь не оказался в точке, с которой начал своё путешествие. Вот так начало пути выглядит сверху:
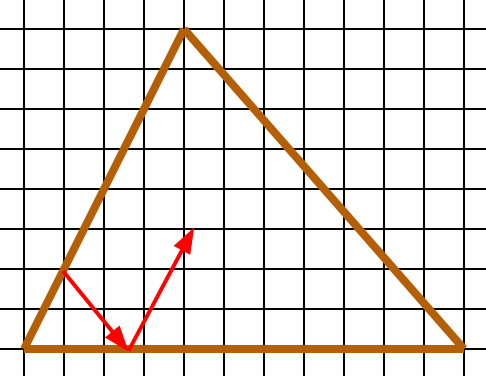
Путь состоит из участков, каждый из которых параллелен какому-то берегу. Какова длина всего пути?
Задача 7.
Встретились пираты Умо, Умо, Амо, Мо и ещё один, имени которого мы не знаем. Каждый из пиратов сказал ровно одну фразу. Вот эти фразы (в каком-то порядке):
- В моём имени меньше букв, чем в любом из ваших!
- Первая буква моего имени идёт в русском алфавите раньше любой из первых букв ваших имён!
- Меня зовут так же, как одного из вас!
- Меня зовут так же, как одного из вас!
- Меня зовут Умо, и мой попугай чертовски красив!
Всё это — чистая правда. Как могли звать пятого пирата? Нужно найти все возможные варианты!

