Задача 1.
Под куполом цирка между консолями натянуты канаты: верхний имеет длину 7 метров, длина нижнего неизвестна (см. изображение).
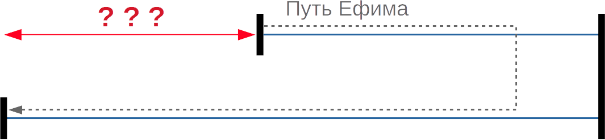
Канатоходец Ефим спрыгнул с верхнего каната, не доходя 3 метров до его конца, развернулся и пошёл по нижнему канату. Всего он прошёл 20 метров.
Найдите расстояние между двумя левыми консолями.
Задача 2.
Фигура «сторожевая башня» ставится во внутренний узел сетки клетчатой доски и бьёт:
- клетки обеих диагоналей, пересекающихся в этом узле
- узлы вертикали и горизонтали, пересекающихся в этом узле
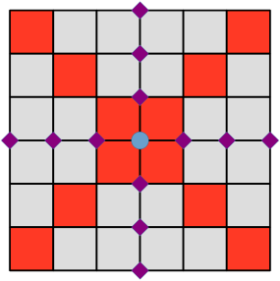
Расставьте как можно меньше сторожевых башен во внутренние узлы таблицы 5 × 5 так, чтобы оказались побиты все клетки и все незанятые внутренние узлы.
Комментарий: Узлы на границе бить не требуется!
Задача 3.
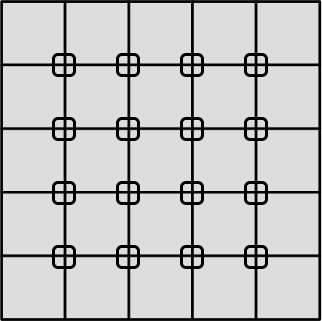
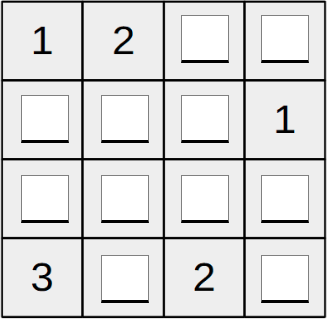
Чтобы открыть тайную каморку, нужно вписать в клетки её замка цифры от 1 до 4. В каждой строчке и в каждом столбце цифры должны быть различными.
Пять цифр уже вписаны. Впишите остальные.
Задача 4.
Встретились как-то на базаре шестеро: каждый из них либо крестьянин (всегда говорящий правду), либо купец (всегда лгущий). Каждый из них сказал остальным пятерым: «Среди вас ровно четыре купца.»
Сколько могло быть среди них крестьян? Укажите все возможные варианты!
Задача 5.
Трое гусар сидят за круглым столом и играют в карты. Перед началом игры каждый гусар положил на стол одну или несколько копеек — свою ставку. Все ставки оказались разными.
Через некоторое время первый из гусар увеличил свою ставку на величину, равную самой большой из ставок его соперников. Затем второй гусар сделал то же самое — увеличил свою ставку на величину, равную самой большой из ставок его соперников. Затем и третий гусар сделал то же самое.
А больше ставки не изменялись: корнет Нечисторуков встал из-за стола, схватил самую большую ставку и сбежал. Какую наименьшую сумму мог он унести с собой?
Задача 6.
Ефим написал на доске число. Подошёл Вася и приписал к нему (то ли справа, то ли слева) ещё одно число. Подошёл Петя и приписал к результату (то ли справа, то ли слева) ещё одно число. Наконец, подошёл Коля и приписал к результату (то ли справа, то ли слева) ещё одно число. Получилось 6567661659.
Числа Васи, Пети и Коли попарно отличались друг от друга не более чем на 8.
Какое число мог написать Ефим? Укажите все возможные варианты!
Задача 7.
Альпинист Касим и бегун Виктор поспорили о том, кто из них быстрее поднимется:
- Касим — по стене на крышу 8-этажного дома
- или же Виктор — по внутренней лестнице на 8 этаж этого же дома
Начинают своё восхождение Касим и Виктор одновременно. Внизу стоит счетовод Ефим с секундомером. Он заметил, что:
- Касим от уровня окон второго этажа до уровня окон четвёртого этажа добрался за 58 секунд
- Виктор оказался на 5 этаже через 2 минуты 12 секунд после начала соревнования
Кто выиграл? На сколько секунд он опередил соперника?
Комментарий: При решении задачи считать, что вертикальная скорость каждого из участников соревнования постоянна, а первый этаж находится вровень с нижней точкой стены.

