Задача 1.
Всем членам одной семьи в сумме сейчас 73 года. Состав семьи: муж, жена, сын и дочь. Муж старше жены на 3 года, дочь старше сына на 2 года. 4 года назад всем членам семьи было в сумме 58 лет. Сколько лет каждому члену этой семьи?
Задача 2.
В словах ЗИМА, МАРТ, ЛЕТО буквы заменены цифрами, причём одинаковые буквы одинаковыми цифрами, а разные – разными. Получилось 3 числа, только, может быть, записанные в другом порядке: 1256, 8763, 9412. А какое число получится при такой замене из слова МИМОЗА?
Задача 3.
12 банкиров приобрели квадратный остров. Они хотят построить на нём квадратный бассейн (который не соприкасается с линией берега), а остальную территорию разделить на 12 равных (по форме и размерам) треугольных участков. Как им это сделать?
Задача 4.
В Хогвартсе, где учатся чистокровные маги и полукровки, за столом собрались более 10 учеников с двух факультетов. Корреспондент спросила у каждого “Сколько за столом магов с твоего факультета?” Все ответили честно, в число магов каждый включил и себя, только чистокровки полукровок за магов не считали. Корреспондент помнит, что среди ответов встретились числа 2, 3, 5, 7, а были ли ещё и другие числа, не помнит. Сколько всего полукровок было за столом?
Задача 5.
Сейчас угол между часовой и минутной стрелкой острый и такой же, как два часа назад. Найдите этот угол.
Задача 6.
Поверхность кубика Рубика 3×3×3 разбита на единичные квадратики. Какое наибольшее число квадратиков можно закрасить так, чтобы они не соприкасались даже углами?
Задача 7.
Разрежьте фигуру на 3 равные по форме и размеру части по сторонам клеток, чтобы в каждой части оказалась 1 звёздочка.
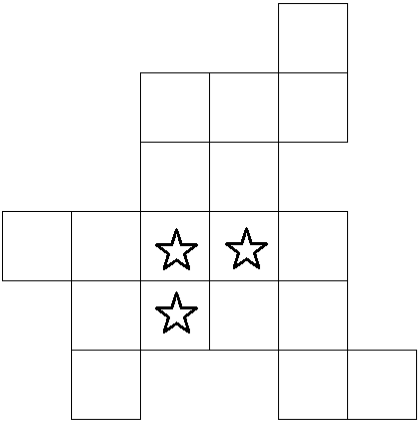
Задача 8.
На поле 7 × 7 клеток спрятался четырёхпалубный корабль (4 клетки подряд в строку или столбец). Можно ли сделать 12 выстрелов так, чтобы точно попасть в этот корабль? Если можно, показать, куда стрелять. Если нельзя, то объяснить, почему.

