Задача 5.
В мешке лежат 12 конфет: шоколадные, мармеладные и мармеладно-шоколадные. Известно, что среди любых 5 конфет найдётся та, в которой есть мармелад. Среди любых 6 конфет найдётся та, в которой есть шоколад. Какое наименьшее число мармеладно-шоколадных конфет может быть в мешке?
Ответ на Задачу 5.
Среди любых 5 конфет найдётся та, в которой есть мармелад. Значит, без мармелада меньше 5 конфет (4, 3, 2, 1 или 0). Среди любых 6 есть такая конфета, в которой есть шоколад. Значит, без шоколада не больше 5 конфет. Чтобы мармеладно-шоколадных конфет было наименьшее количество, нужно сделать максимальное количество чисто шоколадных и чисто мармеладных конфет. Обозначим Ⓜ - мармеладные конфеты, Ⓒ - шоколадные конфеты. Всего у нас 12 конфет. Используя условия, что конфет без мармелада не больше 4, а без шоколада не больше 5:
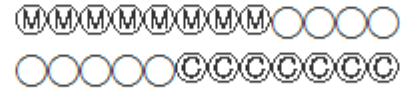
Из рисунка видно, что мармеладно-шоколадных конфет не может быть меньше 3 (перекрытие первой и второй строк).
Ответ: 3 конфеты.

