Задача 5.
Оксана ехала на автобусе и смотрела в окно. Когда автобус проезжал мимо двигающегося навстречу трамвая, Оксана увидела в нём свою лучшую подругу Нику. Они помахали друг другу и жестами договорились выйти на ближайших остановках и пойти навстречу друг другу. Автобус и трамвай остановились одновременно. Известно, что скорость автобуса в 2 раза больше скорости трамвая и в 5 раз больше скорости ходьбы Оксаны и в 4 раза больше скорости ходьбы Ники. Какое расстояние больше: от остановки автобуса до места встречи девочек или от места, где они увиделись, до остановки трамвая?
Ответ на Задачу 5.
Введём обозначения. Пусть скорость автобуса равна 20𝑥, тогда скорость трамвая – 10𝑥, скорость ходьбы Оксаны – 4𝑥, а Ники – 5𝑥. Также введём времена: 𝑡1 – время от момента, когда девочки увиделись до остановки транспорта, 𝑡2 – время от момента остановки транспорта до встречи девочек. Мы знаем, что расстояние=скорость∙время. Напишем в таблицу, кто сколько прошёл и проехал:
- автобус до остановки — 20𝑥∙𝑡1
- трамвай до остановки — 10𝑥∙𝑡1
- Оксана до встречи — 4𝑥∙𝑡2
- Ника до встречи — 5𝑥∙𝑡2
Для бóльшей ясности нарисуем схематичную картинку:
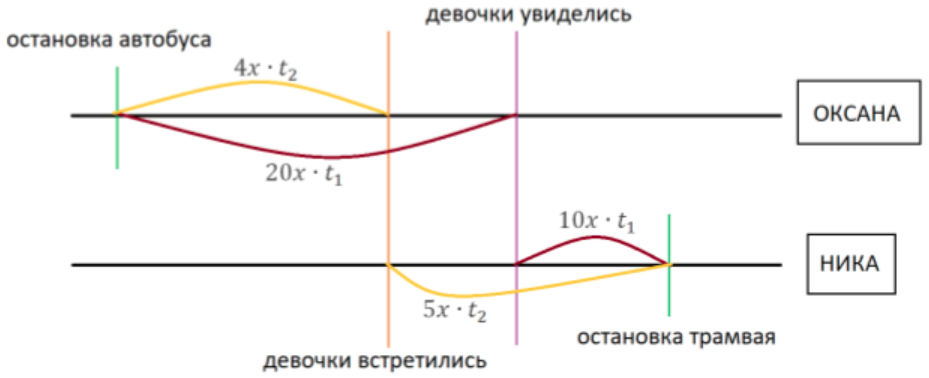
Для того чтобы определить, какое расстояние больше: от остановки автобуса до места встречи девочек или от места, где они увиделись, до остановки трамвая, нужно найти соотношения времён 𝑡1 и 𝑡2. Для начала, наглядно посмотрим, какие расстояния мы сравниваем: от верхней зелёной линии до оранжевой (первое расстояние) и от нижней зелёной линии до фиолетовой (второе расстояние). Из картинки видно, что сумма двух бордовых линий = сумме двух жёлтых. Запишем это:
20𝑥∙𝑡1 + 10𝑥∙𝑡1 = 4𝑥∙𝑡2 + 5𝑥∙𝑡2
30𝑥∙𝑡1 = 9𝑥∙𝑡2
Раздели обе части на 3𝑥:
10𝑡1 = 3𝑡2
Первое расстояние равно 4𝑥∙𝑡2, второе – 10𝑥∙𝑡1. Выразим 𝑡2 через 𝑡1:
𝑡2 = (10 / 3)𝑡1
Тогда, нам надо сравнить два расстояния: 4𝑥∙(10/3)𝑡1 и 10𝑥∙𝑡1. Заметим, что у них есть общий множитель 10𝑥∙𝑡1, но первое ещё умножается на 4 и делится на 3. 4:3>1, значит, первое расстояние больше на 13𝑥∙𝑡1.
Ответ: от остановки автобуса до места встречи девочек больше.

