Задача 6.
Сегодня Оксана празднует свой день рождения. Глядя на календарь, Оксана заметила, что если она сложит две цифры даты и две цифры месяца своего рождения (например, 21 ноября она бы сосчитала как 2+1+1+1) = 5), то получит сегодняшнее число (например, 21). В какой день (дата и месяц) у Оксаны может быть день рождения? Найдите все варианты.
Ответ на Задачу 6.
Запишем дату в следующем виде: 𝑎𝑏.𝑐𝑑.
Заметим, что двузначное число всегда можно записать в следующем виде: 𝑎𝑏 =10𝑎+𝑏. По условию задачи: 𝑎+𝑏+𝑐+𝑑=10𝑎+𝑏. Или же: 𝑐+𝑑=9𝑎. В месяце не бывает больше 31 дня. Значит, 𝑎 может быть равно: 0,1,2,3. Месяцев всего 12, то есть 𝑐 может быть равно: 0,1. Причём, если 𝑐=0, то 𝑑 может быть любой цифрой от 1 до 9, а если 𝑐=1, то 𝑑 может быть только 0, 1 или 2.
Также заметим, что сумма (𝑐+𝑑)⋮9. Единственное число, которое мы можем получить из наших 𝑐 и 𝑑, чтобы оно делилось на 9 – это 9. 9 можно получить единственным способом при заданных условиях: если 𝑐=0, а 𝑑=9. Так как 𝑐+𝑑=9 и в то же время: 𝑐+𝑑=9𝑎, то 𝑎=1. Мы нашли 3 цифры из 4. Запишем, что у нас есть на данный момент: 1𝑏.09. То есть, подходящие даты десятые числа сентября. Проверим, все ли они подходят:
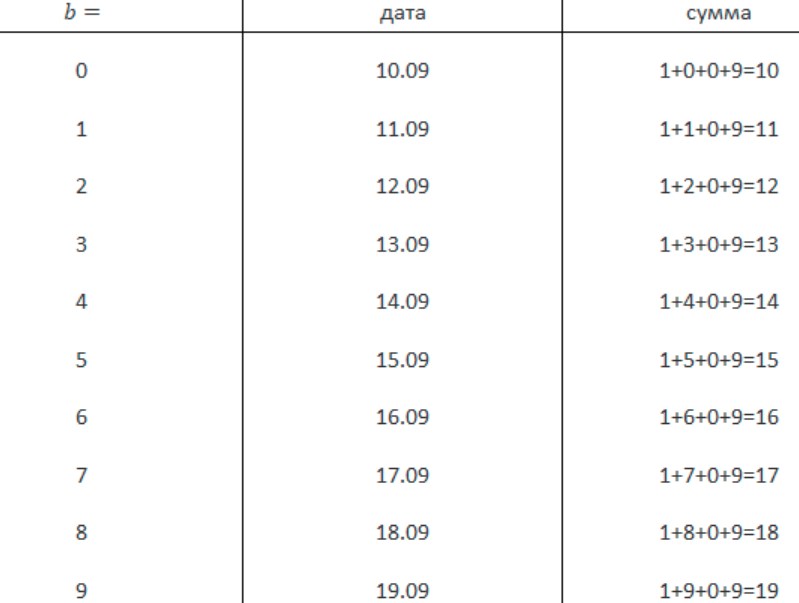
То есть, нам подходят все 10-е числа сентября (10-е включительно).
Ответ: все 10-е числа сентября, 10-е включительно.

