Задача 1.
Найдите все решения уравнения:
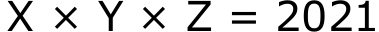
если X, Y, Z — различные натуральные числа.
Задача 2.
Сколько всего пятизначных чисел, в записи которых нет нулей и единиц?
Задача 3.
Вася делил все конфеты, которые ему подарили на Новый год. Четверть конфет он сразу съел. Одну пятую оставшихся конфет он отдал старшему брату. После этого одну шестую оставшихся конфет он отдал младшему брату. После чего у Васи осталось конфет вдвое меньше, чем ему подарили. Какое наименьшее число конфет могло быть у Васи изначально? (Каждый раз Вася отдавал целое число конфет)
Задача 4.
Делится ли число 102021 + 2021 на 3?
Задача 5.
В магазине два ноутбука стоили одинаково. На первый ноутбук сначала сделали скидку 10%, потом сделали скидку 20% от новой цены, а потом сделали скидку 30% от новой цены. А на второй ноутбук сделали сразу скидку 50%. Какой ноутбук в итоге стоит дешевле?
Задача 6.
На плоскости расставили 2021 точку. Далее некоторые точки соединили отрезками. Может ли быть такое, что из каждой точки выходит различное число отрезков от 1 до 2021?
Задача 7.
Разрежьте фигуру по линиям сетки на четыре одинаковых.
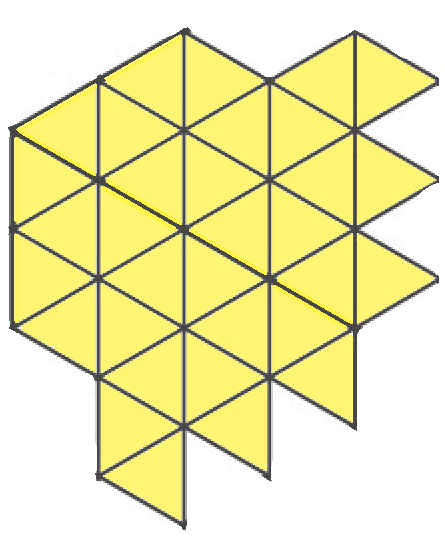
Задача 8.
Докажите, что число 13512966 не является квадратом.
Задача 9.
Имеется нарисованная прямоугольная сетка 1х1. На этой сетке нарисовали пятно, площадь которого меньше 1. Всегда ли можно сдвинуть и повернуть сетку так, чтобы все её узловые точки не были накрыты пятном? (Форма пятна может быть любой, в том числе она может состоять из любого числа отдельных частей. При перемещении сетки клякса остаётся на месте)

