Задача 1.
Можно ли разрезать квадрат 5 × 5 без одной угловой клетки на 5 фигурок “уголок из трёх клеток” и 3 фигурки “полоска из трёх клеток”? Фигурки можно поворачивать и переворачивать.
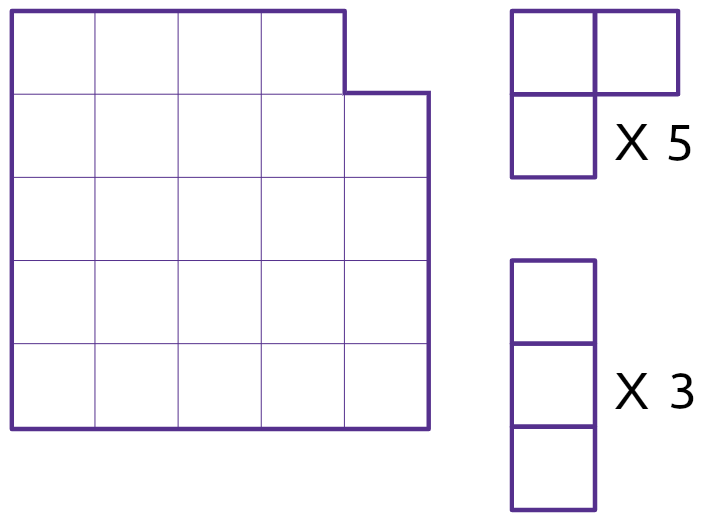
Задача 2.
Волшебник Игнациус вылетел из своего замка в хижину ведьмы Мариши. А ведьма в тот же момент отправилась в замок Игнациуса. Через 10 минут они пролетели мимо друг друга, но не заметили этого. Через двадцать минут (после их встречи) Игнациус был уже в хижине. А сколько минут летела от хижины до замка Мариша? (Их скорости были постоянны)

Задача 3.
На нескольких карточках Вася написал цифру, а с оборота букву (если цифры равны, то буквы одинаковы, если цифры различны – буквы разные). Вася считает сумму цифр на карточках. Если выложить слово ЛОМ, получится сумма 4, МОЛВА – 20, ВОЛ – 10. А что получится в сумме, если выложить слово ВАМ?
Задача 4.
Каждая из 9 одноклассниц узнала по одной новости. Известно, что Анжела разговаривает с Беллатрисой, Велимира с Анжелой и Беллатрисой, Есения с Жозефиной и Земфирой, Велимира поддерживает мир ещё с Инессой и Глафирой, Инесса очень близко дружит с Анжелой, а Земфира с Жозефиной и Есенией, Дарина очень замкнутая и разговаривает только с Велимирой. Больше никто ни с кем не разговаривает, все в ссоре. Девочки болтали целый день, передавая новости тем, с кем говорят, а те передавали дальше. Могли ли к вечеру все одноклассницы знать все новости?

Задача 5.
Есть девять карточек с числами: 1, 19, 33, 13, 79, 5, 99, 61, 43. Поля, Валя и Тина взяли по три карточки. Поля сказала «среди моих карточек самое маленькое число — 19». Валя на это ответила: «Я точно знаю, какие у кого карточки оказались». Кому досталась карточка с числом 13?
Задача 6.
Вася Двоечкин получает за урок 7 двоек, а Петя Пятеркин за то же время – шесть пятёрок. Сегодня они оба пришли в школу к первому уроку и начали получать свои оценки. Васе надоело получать двойки, и он сбежал с последнего урока. Сколько всего пятёрок получил Петя Пятеркин, если он получил их столько же, сколько Вася двоек, и не пропустил ни одного урока?
Задача 7.
Расставьте в клетки числа от 1 до 4 так, чтобы в каждой строке и в каждом столбце все числа были различны, а все неравенства были верными.
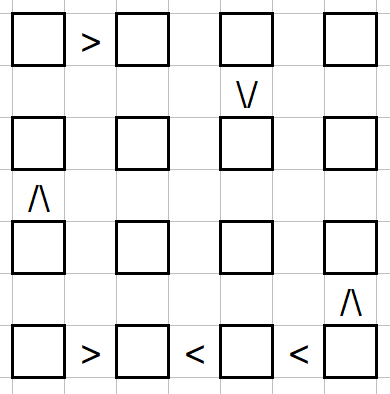
Задача 8.
Разгадайте слово из семи букв, если известно, что между И и А помещается 4 буквы, И идёт раньше А, первая и третья буквы в нём – одинаковые согласные. Т в середине слова, М идёт через две буквы после С, и в слове есть буква Е.
Задача 9.
В клубе собрались джентльмены, которые всегда говорят правду, и мошенники, которые всегда лгут. На одной из встреч клуба каждый присутствующий сказал другим хотя бы одну из двух фраз: “Среди вас не больше двух джентльменов” и “Среди вас не больше двух мошенников”. При этом точно был хотя бы один человек, сказавший обе фразы. Сколько среди присутствовавших могло быть джентльменов, если в клубе в тот день было не меньше 50 человек?
Задача 10.
Знамя Орков представляет собой кусок чёрной материи площадью 180 см². На него с нахлестом нашиты красный и белый дракон. Причем площадь красного дракона 72 см², а та его часть, которая не скрыта белым драконом, 64 см². Голая чёрная ткань составляет 55 см². Какова площадь белого дракона?

