Задача 1.
Можно ли составить выражение, значение которого равно 27, использовав для этого не более шести единиц (другие цифры использовать нельзя), а также операции сложения, вычитания, умножения, деления, возведения в степень и скобки? (не обязательно использовать все знаки и скобки)
Задача 2.
Решите в натуральных числах уравнение:
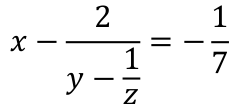
Задача 3.
Во время кораблекрушения на необитаемом острове вместе с неуловимым Джо оказалось несколько пар коз, овец и кур, и для выживания необходимо начать их разводить. Для того, чтобы защитить животных и птиц от хищников, необходимо построить забор. Для кур надо не меньше 30м2, для коз требуется огородить не меньше 45м2, а для овец не менее 55м2. Сможет ли Джо выполнить задуманное, если после кораблекрушения он смог собрать досок на 58 метров забора, а ещё у него осталось 3 прочных двери шириной в 1 метр каждая?
Задача 4.
Легко выбрать несколько предметов из какого-нибудь множества, осуществляя это последовательно, т. е. выбирая сначала 1-й предмет, затем 2-й и т. д. У «Клуба Настольных Игр» возникла задумка сделать это с помощью генератора случайных чисел. Что хотят осуществить ребята:
- Предметы выбираются случайным образом, и ни один из предметов не может иметь преимущество перед другим.
- После ввода параметров (количество предметов в множестве и сколько необходимо выбрать) нажимается кнопка и выдаётся одно единственное число (натуральное от 1 до n, заданного нами), по которому и осуществляется выбор.
Считая, что все предметы, из которых надо осуществлять выбор уникальные (нет одинаковых) придумайте и опишите такой алгоритм и укажите какие числа для него надо ввести для выбора:
а) 3-х предметов из 8,
б) 4-х из 10.
Задача 5.
Докажите, что 2021 + 2122 + 2223 — составное число.
Задача 6.
Площади трёх граней параллелепипеда равны 28 см2, 42 см2 и 24 см2. Найти объём параллелепипеда. Докажите, что этот результат единственный, или найдите все возможные результаты.
Задача 7.
Вася и Василиса играют в следующую игру. За один ход можно нарисовать на стене несколько золотых рыбок, на первом ходе – любое количество от 1 до 2021, на каждом следующем – не больше, чем было нарисовано на предыдущем ходе. Выигрывает игрок, после хода которого на стене будет нарисовано по крайней мере 2022 золотые рыбки. Василиса рисует первая. Кто выигрывает при правильной игре и как он должен для этого играть?
Задача 8.
Аня записала три последовательных натуральных числа. Оказалось, что для этого ей понадобились только три различные цифры, причём одна из этих цифр была использована ровно 9 раз и присутствовала минимум в 2-х из этих чисел. Докажите, что таких троек бесконечное число и приведите их общий вид.
Задача 9.
В ХIХ – ХХ веках Россией правили 6 царей династии Романовых. Вот их имена и отчества по алфавиту: Александр Александрович, Александр Николаевич, Александр Павлович, Николай Александрович, Николай Павлович, Павел Петрович. Один раз после брата правил брат, во всех остальных случаях после отца – сын. Как известно, последнего русского царя, погибшего в Екатеринбурге в 1918 году, звали Николаем. Найдите порядок правления этих царей.
Задача 10.
В детстве жена человека-паука ставила его сына в угол (левый верхний). Когда мама вышла в магазин. Он обнаружил муху сверху двери (где именно, мы не знаем). Успеет ли он поймать муху и вернуться обратно?
Размеры комнаты в метрах 8*3*3 (ДШВ). Дверь находится справа, в середине узкой стены и имеет размер 1*2 метра. Сын человека-паука может передвигаться только по стенам, полу или потолку. Скорость сына человека паука 3 м/ч. Мама вышла на 5 мин (и 3 часа говорила с соседкой).

