В Царском море есть острова, соединённые мостами (изолированных островов нет), один из этих островов называется Загадочный. Каждый из остальных островов тогда и только тогда соединён с островом Загадочный, когда он соединён с чётным количеством островов. Какое количество островов может быть соединено с Загадочным, если всего мостов 7, и между любой парой островов проходит не более одного моста?

Некоторые люди говорят и правду, и неправду, а некоторые определились и либо всегда врут, либо всегда говорят правду. Однажды за круглым столом собрались 6 человек, и каждый произнёс: «Мой сосед справа уже определился». Известно, что в этот день люди одного типа не сидели рядом. Сколько могло быть среди присутствующих тех, кто уже определился и решил говорить правду?

Морской царь полюбил математику и интересные числа. Когда его спросили: «Сколько алмазов в вашей короне?», он ответил: «О, это очень интересное число! Если возвести его в любую степень не выше четвёртой, а потом у получившегося числа посчитать сумму цифр, то получится то же самое, что и при проведении этих действий в обратном порядке. То есть неважно, сначала я посчитаю сумму цифр, а потом возведу в степень, не большую 4, или наоборот, результат будет одинаковым! При этом алмазов больше 1!» Можно ли однозначно определить, сколько в короне алмазов?

Сундук с драгоценностями можно открыть следующим образом: замок в виде красного равностороннего треугольника надо накрыть 6 волшебными синими треугольниками, имеющими такие же форму и размер, как и замок. При этом каждая красная точка должна быть накрыта ровно одним синим треугольником, а синие треугольники не должны пересекаться друг с другом. Как это сделать?

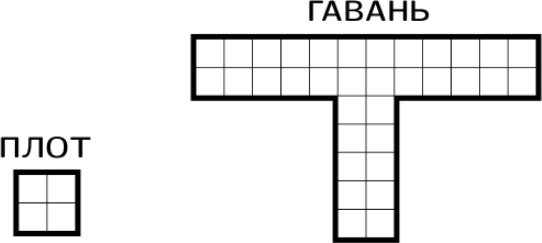
Помогите капитану разместить как можно больше плотов в гавани так, чтобы никакие два плота не соприкасались даже углами. Ответ объясните.

В вершинах прямоугольника 3 × 4, расположенного на клетчатой сетке, отмечены четыре точки. Добавьте ещё одну точку так, чтобы площадь полученного пятиугольника была равна 9 см². Площадь одной клетки 1 см².