! В задаче не хватает рисунка с бланка ответов !

На рисунке ниже изображена деталь. Размести как можно больше таких деталей в коробке, показанной на бланке ответов. Детали не должны накладываться друг на друга.

Каждый год некоторые рыцари двух королевств совершают подвиг. За два года каждый из рыцарей совершил хотя бы один подвиг. На пиру в конце первого года каждый рыцарь первого королевства преувеличил число подвигов, совершенных им за год, в пять раз, а каждый рыцарь второго королевства — в четыре раза. Если верить их словам, то рыцари второго королевства совершили не меньше подвигов, чем рыцари первого. Та же история повторилась и на второй год. Какое наибольшее число рыцарей может проживать в первом королевстве, если всего в двух королевствах 13 рыцарей?

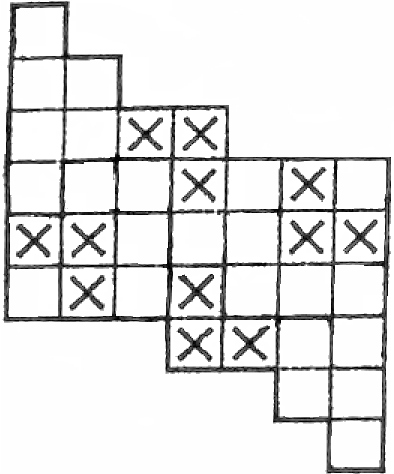
Раздели фигуру по границам клеток на пять равных по площади частей так, чтобы в большинстве фигур большинство клеток было помечено крестиком.

Вася поставил карандаши на одну из граней кубика. Не отрывая карандаша от кубика, он нарисовал линию, которая прошла по всем граням и вернулась в исходную точку. Теперь грани кубика выглядят так:

Нарисуй, как Васина линия пройдёт по развёртке кубика.

Каждый пират либо всегда лжёт, либо всегда говорит правду. Купец же может сказать что угодно когда угодно. Как-то раз Хью зашёл в таверну и услышал, как три человека, кричали друг другу следующее.

• Первый второму: «Ты только что солгал!»
• Второй третьему: «Ты только что солгал!»
• Третий первому: «Ты только что солгал!»
• Первый второму: «Ты только что солгал!»
• Второй третьему: «Ты только что солгал!»

Какое наименьшее количество купцов могло быть среди этих троих?

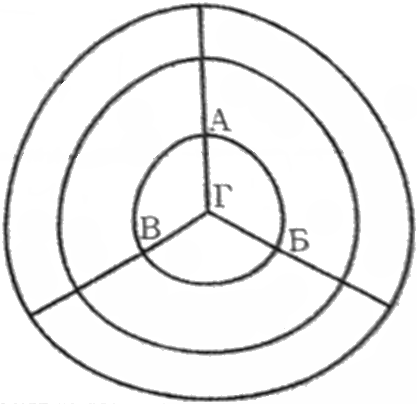
Паук залез на край своей паутины и начал по ней бегать, поворачивая на каждом перекрёстке направо или налево. Побегав, он спрыгнул с края паутины. В перекрёстке А он побывал три раза, в перекрёстке Б — четыре раза, а в перекрёстках В и Г — пять раз. Приведи пример траектории, по которой мог двигаться паук. Укажи, в какой последовательности он посещал перекрёстки А, Б, В, Г.