Задача 1.
Два пирата, Хью и Джон, бегут из темницы. Перед ними коридор длиной 100 метров, заканчивающийся открытой дверью. Известно, что ровно через 10 секунд после того, как кто-то пересекает дверной проём, дверь закрывается. Хью бежит со скоростью m > 0 метров в секунду. С какой скоростью может бежать Джон, чтобы оба пирата выбрались из темницы? Укажите все варианты!
Задача 2.
Каждый год некоторые рыцари двух королевств совершают подвиг. За два года каждый из рыцарей совершил хотя бы один подвиг. На пиру в конце первого года каждый рыцарь первого королевства преувеличил число подвигов, совершенных им за год, в пять раз, а каждый рыцарь второго королевства — в четыре раза. Если верить их словам, то рыцари второго королевства совершили не меньше подвигов, чем рыцари первого. Та же история повторилась и на второй год. Какую наибольшую долю могут составлять рыцари первого королевства от числа рыцарей в двух королевствах?
Задача 3.
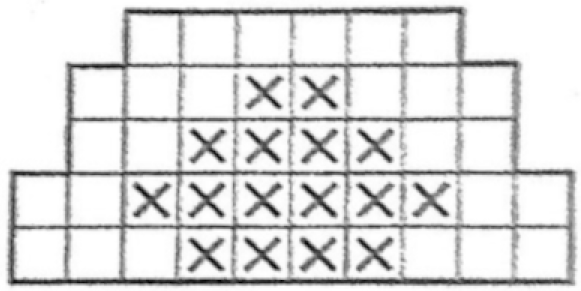
Покажите, как разделить фигуру по границам клеток на семь равных по площади частей так, чтобы в большинстве фигур большинство клеток было помечено крестиком.
Задача 4.
Ровно в полдень любопытная улитка Люба заползла на кончик минутной стрелки (длины 10 см) и поползла по стрелке к её началу. Когда минутная стрелка прошла полный круг и снова соединилась с часовой, Люба оказалась в 7 сантиметрах от центра часов, как раз на уровне кончика часовой стрелки. Улитке стало любопытно, и она переползла на часовую стрелку. Люба заторопилась и за время, прошедшее до следующей встречи стрелок, успела доползти 2 центра часов и вернуться обратно. Здесь она вновь переползла на минутную стрелку и к следующей встрече стрелок с прежней скоростью доползла до кончика минутной. найдите отношение скоростей движения Любы по минутной и часовой стрелкам.
Задача 5.
Собрались как-то 3 мудреца, каждый из которых либо всегда лжёт, либо всегда говорит правду (и каждый знает про себя, говорит он всегда правду или всегда ложь, но не знает этого о других). На каждого надели либо красный, либо синий колпак, но никто не знал, какого цвета на нём колпак. Произошла следующая беседа:
- Первый: «Я не вижу красных колпаков».
- Второй: «Я вижу 1 красный колпак».
- Третий: «Я вижу 2 красных колпака».
- Колпак Третьего: «Среди мудрецов нет того, кто говорит правду и носит красный колпак».
- Первый: «Я до сих пор не знаю, сколько красных колпаков надето!»
На ком из собравшихся были красные колпаки, если мудрецам известно, что говорящие колпаки лгут тогда и только тогда, когда они надеты на лжеца?
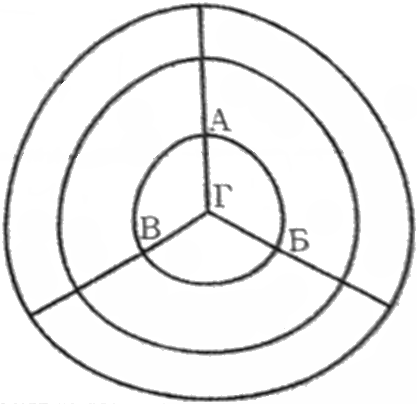
Задача 6.
Паук залез на край своей паутины и начал по ней бегать, поворачивая на каждом перекрёстке направо или налево. В некоторый момент он остановился на перекрёстке и заснул. Известно, что в перекрёстках А, Б и В паук побывал по 2015 раз. Верно ли, что паук заснул в одном из перекрёстков А, Б, В, Г?