Задача 1.
Капитану Флинту нужно разложить золотые слитки по сундукам. В один сундук больше одного слитка не поместится. Ниже изображены слитки и сундуки. Один из слитков никуда класть не надо. Нарисуйте, как слитки должны лежать в сундуках.
Слева изображены слитки, справа — сундуки:

Например, слиток можно положить в сундук так:
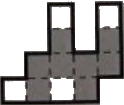
Задача 2.
На Фруктовом острове неделя состоит из 5 дней: Кокосник, Ананасник, Вишник, Бананник, Грушник. Но в каком порядке идут дни, неизвестно. На острове живёт Фит. Фит всегда говорит правду.
- Ананасник ближе к Бананнику, чем Вишник к Кокоснику, — сказал Фит в Грушник.
- Вчера был Бананник,— сказал Фит в Кокосник.
В каком порядке идут дни недели на Фруктовом острове, если первый день недели называется Кокосник?
Задача 3.
Ефим написал в тетради несколько примеров. После чего он положил карточки с треугольниками на все цифры 1, 2 и 9, которые встретились. На цифры 5, 6 и 7 он положил карточки с квадратами. На цифры 0, 3, 4 и 8 он положил карточки с кругами. Посмотрите на изображения ниже и напишите в клеточки, какими могли быть изначальные примеры.


Задача 4.
Пираты построили несколько маяков и нанесли их на карту. Из каждого маяка видны только те маяки, которые не загорожены другими. Поставьте на карту ещё один маяк так, чтобы только у одного маяка изменилось количество видимых из него маяков, а у остальных осталось прежним. Маяк можно ставить только на пересечение линий сетки.
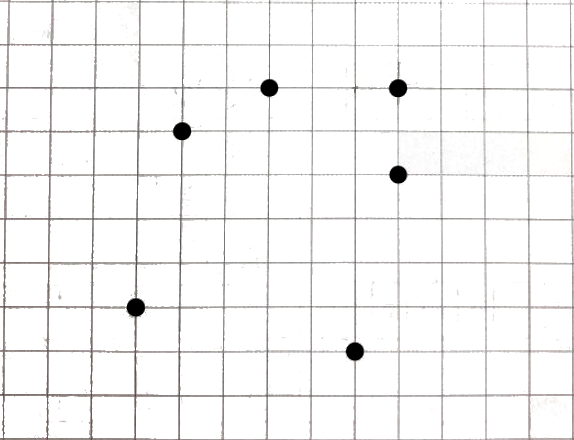
Задача 5.
В порту встретились три капитана: Джек Воробей, Чёрная Борода и Барбосса. Барбосса всегда говорит правду, Чёрная Борода всегда лжёт, а Джек Воробей говорит как правду, так и ложь.
- Первый капитан сказал второму: «Ты не можешь лгать!»
- Третий показал на второго и сказал: «Ты не можешь говорить правду!»
- Второй сказал первому: «Ты не можешь лгать!»
Как звали каждого из капитанов?
Задача 6.
В аквариуме живут осьминоги и наутилусы. Часть наутилусов чёрного цвета, остальные — белого. Некоторые осьминоги сегодня чёрные, остальные — белые. Каждую ночь после полуночи чёрные осьминоги становятся белыми, а белые — чёрными. Наутилусы цвет не меняют. Сегодня в аквариуме 8 чёрных животных и 4 белых. Среди них 3 чёрных наутилуса и два белых осьминога. Сколько белых и сколько чёрных животных будет в аквариуме завтра?
Задача 7.
Попугай Туртур ходит по линиям сетки (вверх, вниз, вправо или влево) от А к Б, от Б к В, от В к Г, от Г к точке А.

Он записал свой путь стрелками, а потом зашифровал стрелки знаками. Одинаковые стрелки заменил на одинаковые знаки, а разные заменил на разные знаки. Получилось 4 последовательности, но какая последовательность к какому отрезку пути относится — неизвестно. Нарисуйте маршрут попугая Туртура.
Последовательности, которые получил Туртур:


