Задача 1.
В одной из пещер необитаемого острова три пирата нашли клад золотых монет, разложенных в мешочки. В первом мешочке было 7 монет, а в каждом следующем — на две монеты больше чем в предыдущем; в последнем мешочке лежало 99 монет. Пираты собрали все монеты в одну куч и принялись их делить. Смогут ли пираты поделить найденный клад поровну?
Задача 2.
Капитан Барбосса нашёл в трюме четыре дощечки, на каждой из которых была написана цифра (все цифры различны). Оказалось, что если наибольшее четырёхзначное число, которое можно из них выложить, сложить с наименьшим, которое можно выложить из них же, получится 12598. Дощечки с какими цифрами нашёл в трюме капитан Барбосса?
Задача 3.
Пираты Амаро, Барт, Шарлотта, Дэниел и Элайза собирали ракушки. Они собрали 2, 3, 4, 6 и 9 ракушек (но мы не знаем, кто сколько). Амаро и Барт суммарно собрали вдвое больше ракушек, чем Дэниел и Элайза вместе. У Амаро и Шарлотты вместе на 2 ракушки меньше, чем у Барта и Элайзы в сумме. Сколько ракушек собрал каждый из них?
Задача 4.
Цифры из спичек выкладываются следующим образом:
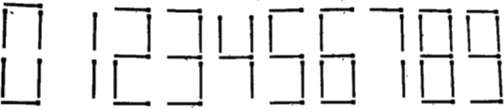
- Найдите все пары двузначных чисел, да таких, что второе из них не просто в два раза больше первого, но и выкладывается вдвое большим числом спичек.
- Найти наибольший палиндром, который можно составить из 2019 спичек. Палиндром — это число, которое слева направо и справа налево читается одинаково.
Задача 5.
В таверне за круглым столом собрались 2019 пиратов, из которых один всегда лжёт, а остальные всегда говорят правду. У каждого из пиратов была либо золотая, либо серебряная монета. Каждому из них задали два вопроса: «Какая у тебя монета?» и «Какая монета у твоего соседа слева?» На первый вопрос ровно 1000 пиратов ответили «Золотая». Сколько пиратов ответили «Золотая» на второй вопрос?
Задача 6.
В сундуке лежат 10 монет достоинствами 1, 2..., 10 франков. Какое наименьшее количество монет нужно вытащить не глядя, чтобы среди них точно попались две монеты, достоинства которых отличаются на 2 франка?

