Задача 1.
Отметьте несколько квадратиков так, чтобы:
- в каждой строчке было не менее 3 отмеченных квадратиков
- в каждом столбце было не более 5 отмеченных квадратиков подряд
- в каждом столбце любые два соседних непрерывных участка отмеченных квадратиков должны быть разделены не менее чем трёмя неотмеченными квадратиками

Задача 2.
Кенга и Крошка Ру прыгают по одной и той же прямой, а Тигра бежит им навстречу:
- прыжок Кенги составляет 380 см
- прыжок Крошки Ру составляет 120 см
- Тигра бежит со скоростью 300 метров в минуту
- начали прыгать Кенга и Крошка Ру одновременно из одного и того же места
- через минуту после начала движения они в первый раз за время движения приземлились одновременно в одно и то же место
Встретились с Тигрой Кенга и Крошка Ру в тот момент, когда они в пятый раз приземлились в одно и то же место.
На каком расстоянии изначально находился Тигра от Кенги и Крошки Ру?
Задача 3.
Капитан Сильвер набрал странную команду: в ней есть исключительно честные пираты, всегда говорящие правду; есть в ней вруны, которые всегда лгут; также есть в ней мудрецы: они говорят правду тогда и только тогда, когда последняя услышанная ими фраза является правдивой.
Как-то встретились в трюме трое пиратов, и завели разговор:
- Кью: У вас обоих есть попугаи.
- Пью: У Гала есть попугай.
- Хью: Нет у меня попугая!
- Кью: Среди нас есть врун!
- Хью: Я не врун!
- Пью: И я не врун!
- Кью: Среди нас нет врунов!
Кто мог быть кем в такой ситуации? Нужно найти все возможные варианты!
Комментарий: Если мудрец говорит первым, то нам неизвестно, какую фразу до этого он мог услышать: поэтому допустима любая истинность высказывания мудреца.
Задача 4.
В пропуски нужно вписать числа 1, 2, 3, 4 (в каждом из равенств каждое из этих чисел — по разу) так, чтобы равенства стали верными:
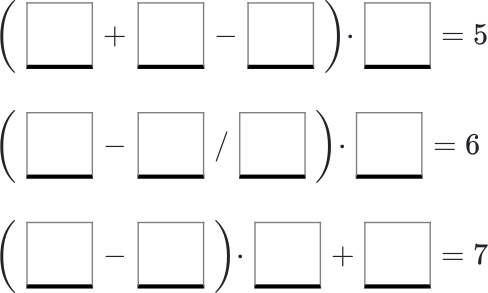
Задача 5.
На сундуке волшебный замок, на котором изображены три овала и три луча, выходящие из одной точки и пересекающие все эти овалы:
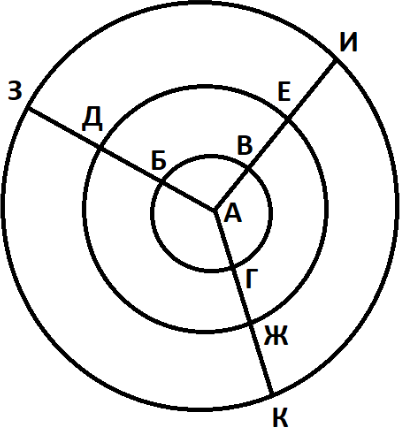
Чтобы открыть сундук, нужно поставить палец в начало лучей (обозначенное буквой А на схеме), затем вести палец вдоль линий, обязательно меняя направление на каждом пересечении (например, проведя палец от Г к Ж, нельзя его продолжить вести к К).
Али-Баба как-то открыл замок, но как — не помнит. Единственное, что он помнит — это то, что его палец побывал в точках Б, В и Г по три раза в каждой.
Какая из обозначенных точек могла оказаться последней на пути пальца?
Задача 6.
Дерево-квадерево имеет квадратное поперечное сечение с квадратными же кольцами на нём. Например, сечение дерева-квадерева с пятью кольцами (центральный белый квадрат тоже считается «кольцом») выглядит так:

Зведочёт Ефим после долгих поисков нашёл пень такого дерева и после долгих изысканий выяснил следующее:
- на пне 4 кольца
- обхват пня равен 96 локтям
- для любых двух соседних (касающихся друг друга) колец площадь внешнего кольца (именно «кольца», то есть квадрата с квадратной дыркой) равна площади внутреннего кольца (которое является квадратом без дырки только в случае центрального белого квадрата)
Каков обхват центрального кольца (центрального белого квадрата)?
Задача 7.
Капитан Флинт очень любит сундуки. Каждый сундук имеет форму прямоугольного параллелепипеда, стороны которого выражаются целым числом метров.
Капитан за долгие годы плаваний собрал все возможные сундуки объёма 18 м3, каждый — в одном экземпляре.
Он хочет расставить их в цепочку вдоль стены, уперев друг в друга и в стену так, чтобы цепочка оказалась максимально возможной длины.
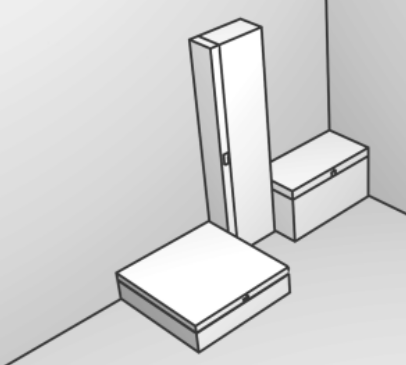
Какова эта длина?
Комментарий 1: Сундуки размерами 1 × 3 × 6 и 6 × 1 × 3 различны: первое число указывает длину сундука, второе — ширину, третье — высоту. При этом ставить сундуки на пол можно на любую из шести граней.
Комментарий 2: Объём сундука можно вычислить, перемножив его длину, ширину и высоту.

