Всероссийская олимпиада школьников по математике, 8 класс, 2015 год, 2 этап
дата проведения: 19 октября 2015 - 25 октября 2015
Задача 5.
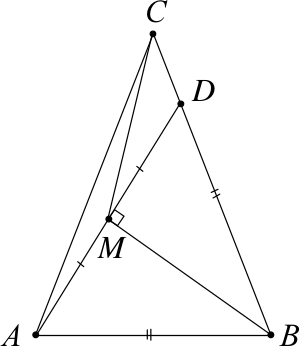
В равнобедренном треугольнике $ABC$ с основанием $AB$ на стороне $CB$ выбрана точка $D$ так, что $CD$ = $AC$ – $AB$. Точка $M$ — середина $AD$. Докажите, что угол $BMC$ — тупой.
Ответ на Задачу 5.
Решение:
Так как $CD$ = $AC$ − $AB$ = $BC$ − $AB$, получаем, что $DB$ = $AB$, а значит, треугольник $ABD$ равнобедренный. Тогда его медиана $BM$ является и высотой, т.е. угол $BMD$ прямой. Значит, $∠BMC$ = $∠BMD$ + $∠DMC$ = 90° + $∠DMC$ > 90° тупой.