Всероссийская олимпиада школьников по математике, 9 класс, 2015 год
дата проведения: 19 октября 2015 - 25 октября 2015
Задача 5.
В треугольнике $ABC$ медиана, выходящая из вершины $A$, перпендикулярна биссектрисе угла $B$, а медиана, выходящая из вершины $B$, перпендикулярна биссектрисе угла $A$. Известно, что сторона $AB$ = 1. Найдите периметр треугольника $ABC$.
Ответ на Задачу 5.
Ответ: 5.
Решение:
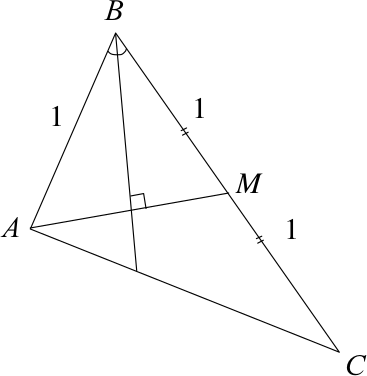
Пусть $AM$ — медиана, проведённая из вершины $A$. Тогда в треугольнике $ABM$ биссектриса угла $B$ перпендикулярна стороне $AM$, т.е. биссектриса является и высотой. Значит, этот треугольник равнобедренный, $AB$ = $BM$ = 1. Но тогда $BC$ = 2$BM$ = 2. Аналогично из второго условия получаем, что сторона $AC$ в два раза больше $AB$, т.е. периметр треугольника $ABC$ равен 1 + 2 + 2 = 5.

