Задача 4.
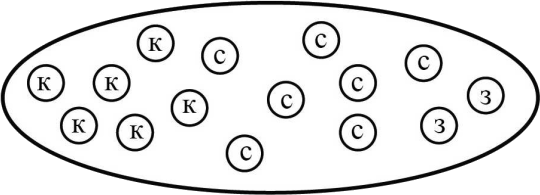
В мешке лежат 15 шариков (см. рисунок). Раскрасьте каждый шарик в один из трёх цветов: синий, зелёный или красный — так, чтобы два утверждения были верны, а одно неверно:
- синих шариков на один больше, чем красных;
- красных и зелёных шариков поровну;
- синих шариков на 5 больше, чем зелёных.
Напишите подробно, как вы рассуждали.

Ответ на Задачу 4.
Ответ: 7 синих шариков, 6 красных шариков, 2 зелёных шарика.
Решение:
Докажем, что второе утверждение не может быть верным. Действительно, пусть верны первое и второе утверждения. Тогда если забрать один синий шарик, то шариков всех цветов должно остаться поровну.
Но 15 − 1 = 14 шариков не делятся поровну на 3 цвета. Пусть теперь верны второе и третье утверждения. Тогда если забрать 5 синих шариков, то опять шариков всех цветов должно остаться поровну.
Но 15 − 5 = 10 шариков не делятся поровну на 3 цвета. Таким образом, могут оказаться верными только первое и третье утверждения. Далее можно рассуждать по-разному.
Первый способ.
Если в мешок положить 1 красный шарик, то синих и красных станет поровну, а если положить ещё и 5 зелёных, то количество шариков каждого цвета будет одинаковым, а именно будет по (15 + 1 + 5) : 3 = 7 шариков каждого цвета.
Теперь можно посчитать, сколько шариков каждого цвета было в мешке: 7 синих шариков, 7 − 1 = 6 красных шариков и 7 − 5 = 2 зелёных шарика.
Второй способ.
Из верных утверждений 1 и 3 следует, что зелёных шариков на 4 меньше, чем красных. Уберём из мешка 5 синих шариков и 4 красных шарика, тогда количество шариков каждого цвета будет одинаковым, а именно будет по (15 − 5 − 4) : 3 = 2 шарика каждого цвета. Таким образом есть в мешке было 2 зелёных, 6 красных и 7 синих шариков.
Возможно также решение с помощью уравнения.

